The Creation of Time

Maeshowe and the Pyramid, both without compare

 

Maeshowe and Giza

These two pictograms are meant to show that the same principles of geometry underlie the designs of the Great Pyramid in Egypt and of Maeshowe megalithic chamber in Orkney. The Maeshowe theorem sets the basic rules that govern the design of the Great Pyramid and the chamber was, most probably, built earlier, but possibly even about the same time.
[The two outer circle pairs in these pictograms (above) do in fact have the same ratios, although it does not show properly in the Maeshowe version for technical reasons]

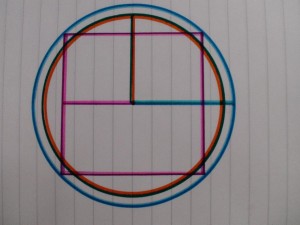
In this chapter it will be shown that the crucial ratios of Maeshowe and the Ring of Brodgar are to be found in two pyramids at Giza, the Great Pyramid and Third Pyramid. As shown in the chapter ‘the Rainbow Proportion’, Maeshowe exemplifies: a. the rule that inscribed and cirumscribed circles and squares always double in area, being a characteristic of the ’11 over 7′ geometry, combined with b. the rule that squaring the circle by circumference [here the turquoise square becoming the red circle, that is, one-dimensional (1-D)], results in a ratio of diameter and diagonal of 10:9, being a characteristic of the ’10 over 9 geometry’. Brodgar exemplifies the solution to the irrationality of square root two in the numbers 140/99 and 99/70. (its diameter is 2 x 99ME= 103.67m).

It is claimed here, probably for the first time, that the (small) Third Pyramid (Menkaure/Mycerinus) is, although deemed to be built later, mathematically the key and the conceptual prototype of the Great Pyramid, in the proportion 9:20 (126:280 and 198:440) and that the Third pyramid holds the same numerical proportions as are laid down (for different units of length) in the Ring(s) of Brodgar, possibly later.

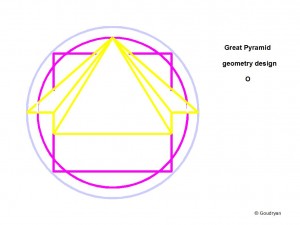
In the first picture (below) the theorem is brought back to the essentials, which still express the full integrated theorem, that is, the full integration of the ratios 10:9 and 11:7 expressed in one pictogram

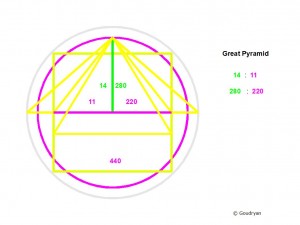
The geometry of the Great Pyramid is the transformation of a (hemi-)sphere into straight lines; the height of the pyramid (280RC) represents the radius of a sphere and the perimeter of the square pyramid base (4 x 440RC) represents the circumference of the same sphere (1760 RC). The Earth.

It has been claimed before that the perimeter of the Great Pyramid is meant to represent a half arc minute of the circumference of the earth: 2 x 60 x 360 x 1760 x .5236m (RC) = 39,810,355 metres. This outcome is wrong by about 250 km, the French though, about 5000 years later and two centuries ago now, were wrong by about 70 km!

In the ‘10-over-9 geometry’ it is the square as 1-D perimeter, equal to the orange circle circumference, which symbolizes the factor: 9; in the ‘11-over-7- geometry’ it is the purple square as 2-D area which symbolizes the factor: 11 (instead of square 7), that is 11×11= 121, whereas the green circle is 7 x 7 x 22/7= 154, so these form an area ratio 11 : 14.
[( Note here that this is a reversal of the ratio of the circle-area inscribed in the square, where the square is 14 and the circle 11, or the square-area inscribed in the circle where the square is 7 and the circle 11, so the numbers 7 (14) and 11 here swap from linear to circular and viceversa. We will see later on elsewhere why this is crucial.)]

 

In this picture we see the complete integration of the ratios 11:7 and 10:9 in an intricate way; the ratios are expressed in the colours of the lines, which sometimes have two colours (9 and 11=purple; 10= blue; 9=orange; 7=green=14).
The ‘blue and orange’ circle symbolizes the ratio of radii and circumferences 10:9, the purple square and the green circle symbolize the area ratio 11:14, they have the same perimeter length. [ half the side of the purple square is 11, so the full side is 22 and the perimeter 88]. The confusing thing here is that this is about ratios, not actual lengths, otherwise it could not be brought in one representation.
The two radii, green=14 and orange= 9 are equal in this representation, but they function in the different ratio systems. Out of this fact follows the crucial ratio number 126 (9 x 14), which is the bridge between the two geometries, 11 over 7 and 10 over 9; it is where the two ratio systems meet and ‘resonate’.

This basic geometrical integration, the ‘geometry of square root(2)’, I have called it, is the ‘raison d’etre’ of the Third Pyramid because it ‘explains’ the foundation of the logic of the Great Pyramid, as Brodgar’s Rings do explain the logic of Maeshowe’s ratios.

 

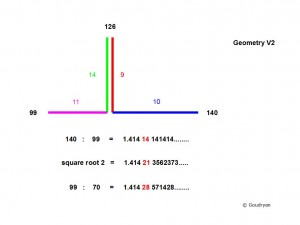
This crucial measure and value forms the top of the Great Pyramid, 126 Royal Cubit (RC) high (=65.97m), from airshaft exit level, and holds the keys to the geometry; 126 is the number for the diameter of Brodgar in Megalithic Yards( 126 MY).
Nine times the side of our initial (purple) square is 9×22= 198 RC, this is the supposed length of the east side of the Third Pyramid (103.67m) at platform level and it is the diameter of the stone circle of Brodgar in Megalithic Ell (198ME). These 198RC sides provide the Third Pyramid with a diagonal of 280 RC ( square root of 198 x198 x 2= 280 RC) at indicated pavement level, which is the height of the Great Pyramid. Half of this Third pyramid base diagonal is 140 RC, which relates to the height of 126 RC as 10:9. QED.

The Third and Second Pyramid heights add up to 126 + 274 = 400

So we see that the Ring of Brodgar and the Third Pyramid express the same basic mathematical theorem in the same lengths. The pyramid expresses a sphere, which the stone circle does not necessarily do, but both are based on exactly the same geometrical principles, because the same numbers are involved (and fortunately the practically same units of measurement!). The stone circle expresses the three values: 126, 198 and 280 (and 350), in one diameter, and in one dimension, by means of three (4) units (meagalithic yard, ell, remen, foot); the Third Pyramid expresses the values with one unit in three dimensions and symbolizes a hemisphere of radius 126 Royal Cubit. It nails down the crucial numbers 99, 126, 140, as the smallest units in which the geometry can be expressed, as it does at the top of the Great Pyramid from airshaft exit level.
In the Great Pyramid we find these ratios in the height as 280RC (20/9 x126), the side as 440RC (20/9 x 198) and in the diagonal of 880 Remen ( 20/9 x 280 = 622.2 RC= 325.78m), which is the circumference of the stone circle of Brodgar.(22/7 x 280 MR= 325.82m). So we see that all these geometries appear to hang together because of the utterly enigmatic equality of the units of length used by two cultures which in all manner could not be further apart than they were.

Corners, angles and slopes of the actual building

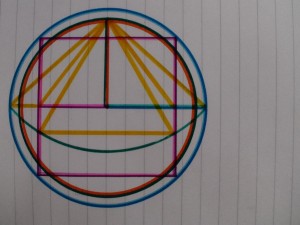
The true proportion of the side of the pyramid, ‘front’ triangle, is defined by drawing a circle segment from the top of the pyramid, as shown in the next picture.

Circle segment is drawn from top of pyramid and connects corner points of the pyramid, like the blue circle does in the perpendicular diagonal section.

The green/orange circle is the sphere the Pyramid represents, the Earth
Half a sphere halved in which the pyramid is also halved.
All true ratios, angles and slopes in a glance

The Pyramid as the gem it is.

The geometry of square root two

Below we find the crucial measurements in the designs of Maes Howe and the Great Pyramid. In Maes Howe only the 10:9 ratio is explicit, in the Great Pyramid the 11:7 ratio is explicitly integrated through the measure of the four sides, 440 RC, which is a multiple of eleven. This symbolizes the ‘number-inversion’ from circle to square, from circle segment 11 (22) to straight side 11.

The Third Pyramid embodies the mathematical theorem in its ground state where the 11:7 and 10:9 geometry are integrated in the basic measurements, like (height) 126 as 9 x 14 and (side) 198 as 2 x 9 x 11 and 280 (diagonal) as 2 x 10 x 14. (the first 5 primes, 2×5, 3×3, 7, 11, 2×7)

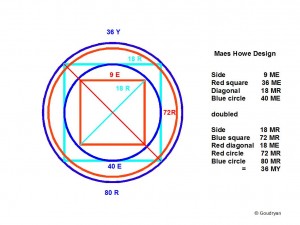
This pictogram of the mathematical ‘anatomy’ of Maes Howe shows best how the two square-root-related units, Megalithic Ell and Remen, guarantee whole numbers throughout the geometrical model. Throughout we see also that the model applies with a striking harmony of numbers and interlocking levels. Note that all the numbers that occur are essential in the theorem, it is all multiples of 9 or 10. Note also the diagonals which hold the proportion.

The outer blue circle circumference in the design of Maes Howe is equal to the inside diameter of Stonehenge, that is 36 MY or 80 MR (29.60m)

 

The anatomy of the Third Pyramid (Menkaure/Mycerinus, below)

Here we see the principles of the Great Pyramid and the Third Pyramid in relation to square root(2). This is the irrational made rational. (see Rationalizing the Ir-rational)
Had Pythagoras known this solution the irrationality of the square root of 2 would not have pained him so much maybe and the history of mathematics would have been different. It is really time mathematicians get a feel for this extraordinary numerical framework for geometry, it’s been used before, has hidden relations.

© Goudryan 2009/2013