Remarks:
the number logic that I laid bare is an algorithm strictly limited to the integrity of natural numbers; irrational and transcendental numbers do not occur, They are neutralized, with the exception of (Pi-) Qute as factor to ‘rationalize’ square roots of 2, it is -> 20V2/9 = 2.22..V2 = 3.14 26 9680… and of Pi-Trite as factor to rationalize square roots of 3 would be:
‘Pi- Trite’ = 3 x 11 x 11 x V3 /2x10x10= 363V3 / 200 = 1.815V3 = 3.14 36 72 2… (1815= 3 x 5 x 11 x 11 ).
Pi x V3 = 5.441.. -> 5.4444 = 49/9 V3/Pi = 0.551… -> 0.55555 = 5/9 Pi /V3 = 1.8137 -> 1.818181 x 99 = 180 : 99
We see that we still keep to the small primes and key numbers, when we discard irrationals.
So ratios of natural numbers are at the core of this lean method.
The inevitable differences in outcomes which occur in this method turn out never to exceed the thousandths and are predictable from the outset. Once a data is adapted to the rules of the system, it can go anywhere to sustain the system; this gives us the freedom to infer any numbers, usually after the second digit, which in most cases will be forming a repetition to create a natural number by means of 99.
( example: 5sqrt(2) = 7.07 106... changes to 7.07 0707... x99= 700 so 700/99 =~~ 5V2; all the odd numbers multiplied by V2, except 7, and adapted, will, multiplied by 99, deliver a striking natural number, like: 3V2= 420/99 ; 9V2= 1260/99 ; 11V2=1540/99 ; 13V2= 1820/99 ; etc.
Great and consequential exception is 7V2 = 9,899 49.., which forms the pivotal -> 9.9 and of course is a ‘natural root’ in factor 99, that is the bridge between the 10/9 and 11/7 calculus and the key to the ambiguous rationality of V2, as being either 99/70 = 1.414 28 57 or 140/99= 1.414 14 14…, where (99/70+140/99)/2 = 1.41421356 4 21356 4 21356 4 . This is a rational approximation of 8 digits, what more do you ever want outside precision science.
V2 = 1.41421356 2 … Period 213564 = 3 x 7 x 11 x 13 x 37 x 37 See here the prominent 37 that plays everywhere behind the scenes, mainly in close relation with the linchpin prime 3, together they form the repunit 111 (R3), following 11 (R2). Repunits are the gatherings of fixed clusters of prime numbers that are basically based on the logic of a ( 100^n ) -1 = 999…..999.
These 9 repdigits divided by 9 gives the order of the repunits and all of all primes except 2 and 5.
(Riemann’s zero’s might be a complement to all primes being factor to repunits. The repunits are the products of the primes in volved in the repunit.
Favorit is R6 this repunit houses 3 x 7 x 11 x 13 x 37 = 111 111 1 /7 = 0,142857 142857 …. 3x11x13x37 = 15873
The repunit is the reciprocal of a cluster of always the same primes, that will never occur in any other setting of primes.
3 and 37 are bonded in 111, that is why the awkward prime 37 (also involved in enigma 137) is such a prominent prime in this logic of natural numbers.
******
In this chapter I want to explain the basis and background of the mathematics I have used throughout this website.
********
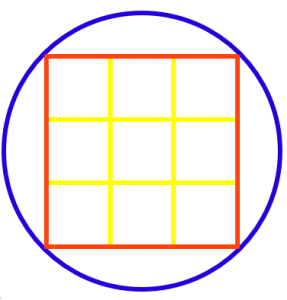
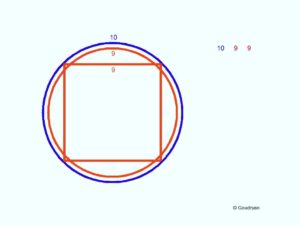
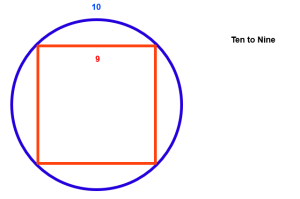
This vignette symbolizes the the quintessential ratio: 10 : 9, with a circumference of circle 10 and square perimeter of 9, or, more explicit , an arc of 10 over a chord of 9. This is, I think, directly related to my most original finding,- although its ratio in diagonal and height of the great Pyramid was observed and mentioned by Lauer, but not elaborated upon, – this finding is that the square area can be interpreted as the surface area of a horn-torus.
This geometric relation, which, because of resonance conditions, has essential tolerance at the most profound levels, gives us the key and reveals an inevitable 10 : 9 ratio.
That is what I have done and it shows that the ratio is intrinsic in the geometry that unfolds from a Pi-value of the rational number 22/7 = 3.142857..142857.., the rationale of the Great Pyramid dimensions, to express a half sphere, purportedly the earth itself of which they surmised a circumference only 200km short of the now established value.
Below we see the red circle 9, with the ninth square of same perimeter
The mathematical model I have ‘uncovered’ is a natural number logic with complete complementary integration and consistency and, in that sense, unassailable. Its principles are very simple and you might enjoy these ‘clean and clear’ numbers , that , you never knew, were just around the corner in many designs you have appreciated for their inner harmonies. (“why did nobody tell us this?”).
The only fundamental difference with established mathematics is the crucial premise that only natural numbers be used and that the difference with established math never exceeds the ‘9-thousandths’, (usually the third digit) which turns out to be a matter of course of the model itself, it creates its own ‘laws’.
The integrity of the natural number and its ratios is paramount and preserved.
Apart from being a tool of mathematical harmonics, think of music, the natural numbers are basic to the phenomena of resonance and wave interference. This already shows fields follow natural number order. This is the ultimate rationale for taking this odd “Kindergarten-model’ seriously, it may tell scientists something fundamental about the geometry of space, of ‘real’ space, not abstract space, so, the domain of the numbers.
[[[It is good to realize that the way we represent geometry with dots, straight lines and curves, does not make these tools intrinsically real, we have objectified the distance between two points by drawing the shortest distance in between. In our conceptual framework the line is rigidly straight, as it shows, but when there is no real line the shortest distance between two things, that are both in fundamental vibration, must vary; this variation may be small but it is there, it depends on the geometry of local space; so the ‘rigid preciseness’ of irrational numbers is superfluous, a farce, in this environment, though their squares are welcome and their irrationality is duly ‘rationalized’.]]]
What for me became the deciding moment was when I found that the square is a 2-D representation of the surface area of a horn-torus, and that that relation is expressed in the square having identical perimeter as the circle. This transformation is one of the key dynamics of geometry of space, is the claim here, because we see the spherical and toroidal shapes in our everyday reality
The essential thing of this whole geometry is that it anchored the ratio 10 : 9 in a basic geometry concerning the mutual ratios of squares and circles, and eventually of horn-tori and spheres. The fact that the ratio 9 to 10 holds for any circle or square is its universality and creates a logic of its own. It means that the ninth square had perimeter 9, but the 9th circle around the ninth square has circumference 10. It is the perimeter of the tenth square as 10 which makes it equal to the the ninth circle, that is also 10 This is the resonance of the ninth Sphere with the tenth (horn-) Torus as ratio 9 : 10 that is the only logical mechanical explanation.
Let’s first clear up the 2-D intricacies before going back to reality.
In the Great Pyramid, the height is the 9 and half ground diagonal is the 10, the whole diagonal is the 20, as ratios. Height is 280 RC = 396 Royal Remen and the diagonal is 880 RR , one value is divided by 9 and gives 44 and, the other divided by 10 giving 88, these all point to 11 as the Cardinal number, the arc over 7, as the 22 of the Pi- formula 22/7, and indeed 7 (-14) is the other pillar of this geometry and to be found as radius of the globe in the height of 280 RC, (which cannot be properly divided by 9) and the circumference of the globe in 1760 RC = 4×440 . 1/2 diameter = 280RC and half the circumference is 880RC, so here we see the indomitable 22/7 verified in architecture again : 880 / 280 = 22 / 7. QED
Here now we have engraved the calculator that reveals the radius and circumference of the earth by using the squaring of the circumference of a circle.
All this logic stems again from the universal relation of 9 : 10 of straight side with a quarter arc spanning it, like 11 spans the diameter of 7 to give a half arc. The 10 over 9 is a beautiful arc, where 11 over 7 has a more cosmological ring about it, the perfect arc
The next stage is when we start to integrate 11:7 with 10:9 ratios
With P as 22/7 the surface areas of squares and circles become very simple. A square of 7 fits a circle of 11 exactly and so does the square 14 fit around circle 11. When we square the circle by circumference , the resulting square relates as 11 to the (squared) circle 14, so from 7, 14, 28 etc. for the squares, now the squares are 11, 22, 44 etc. So there is a deep transformation when square and circle morph int0 one another.
(Picture squared circles, 14/11?)
Depending on the context the approximations may give a better view of the dynamics of any ‘real’ situation in the presence.
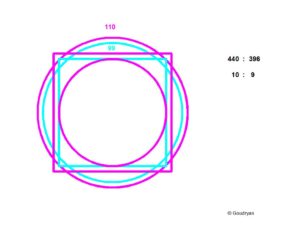
We see here in turquoise a square of side 99 and a circle of the same circumference as the square, also 396 (4×99)
Then there is an ‘electric purple’ circle with circumference 4×110 = 440 and the same coloured square of sides 110. We see that these pairs reflect a ratio of 440 : 396 = 10 : 9 . The ratio between the diameter of the inner purple circle and the next turquoise circle is what I call the (double-) Rainbow Proportion, it is 11 : 14. How do we distil this from the data above.
Here picture of 9 and 10 squares and the relation 1.62.
To reach a ratio 9 : 10 we have to to cut the diagonal of square-9 by 1/10th so : 9V2/10 = 1.2727…x 99 = 126/99 = 14 : 11 dat is 14/11 deel van diagonaal kleiner voor de diameter van de vierkant-9-cirkel (niet 9e cirkel want die is 10)
The core of my system boils down to the fact that any circle made into a square by same circumference, will have a diameter that is 9/10 the length of the square’s diagonal. This simple ratio of diagonal and diameter being 10 : 9 is the key to the natural number mathematics I have developed. This is the complement of the fact that the quarter-circle arc that spans a base of 9 is 10.
The circumference of a circle 10 will have an inscribed square with perimeter 9.
when we take 12.727 – 1.2727 = 11.4545/2 = 5.72727… -> 2 x 5.727 x 22/7 = 36 so this circle has indeed the value 4 x 9 = 36 circumference of the square 9
radius inner circle 4.5 , thus ratio inner circle and square-9 circle is 5.727 : 4.5 = 1.2727 = x 11 = 14 .
So Rainbow proportion is always 11 ; 14 or even 1 : 1.62 as regards the areas; see also (14/11)^2 = 1.6198.. (1.618..phi)
We see here how the golden ratio is clustered with different backgrounds
(( I’am not happy with this text on review in 2025, i cant manage it anyore)
(picture)
You will know the formula for a circle circumference as 2.pi.r and you may have heard of the notorious ‘squaring the circle’, but you probably don’t know the square of the formula being 4.pi^2.R^2, which happens to be the square of 2.pi.r . And what might that look like you may wonder. Well, it is two circles in intimate relation, it is one circle tangent to an axis, circling its own centre, a horn-torus. The whole image is dynamic because the longitudinal bulge-circling is around the centre of the plane circle of the tangential circling, so to speak. These circles are fundamentally interlinked. They never touch, they symbolize the impenetrable space in these dynamics of the horn-torus and anything toroidal.
we do not recognize the geometric dynamics of the torus in reality we are with ease with balls and circles, but the torus brings in the ‘linear’, its surface is a mathematical straightedge in 2-D, this way the torus without a hole, in 2 D is a square!
(picture horn-torus)
(Link met Daeumler , Remark on the dynamic horn torus model in (quantum) physics.))
The small difference I found between 9 and 9.0031 (just over 3 thousandth) in the circumference of a square inscribed in a circle of 10, was the trigger of this whole endeavour to clear the way for natural-number-priority in the workings of nature. This can be shown in the ratios of the solar system and is spectacularly displayed by the rings and gaps of Saturn’s razor-thin Euclidean plane ring system.
(pictures)
This model purports to explain the occurrence and function of resonance as one of the basic conditions for ordering space and ‘creation’ of matter. The model concentrates on the ratios of circles and squares, 2-D, as representatives of spheres and horn-tori in 3-D. It is these basic geometric forms which are supposed to comprise the backbone of the dynamics in the geometry of space. (There would be 5 dimensions, but no time dimension, because the two perpendicular circular (vorticular?) dimensions allow a measurement of time, that is, rate of change; this is a tentative explanation.
We see that the model has universal explanatory application. From the geometry and quanta of space, to the resonances of the solar system and lunar orbits around planets, from resonance to memory and awareness, to sympathy and agreement. What the model does is give an essential confirmation of Pythagoras’s conviction and insight that ‘all’ was a matter of number. Importantly rational numbers, comprising the ratio of two natural numbers, were seen as quintessential, which showed in the mathematical harmonics of music. The two pivotal rational numbers in this model are 11/7 and 10/9, and everything follows from their complementarity. It’s amazing.
The one is the half arc over the diameter, 11 over 7, the other is quarter arc over the chord as side of the square, 10 over 9 (2×5 / 3^2) : the arcs over triangle-, pentagon-, hexagon- and octagon-sides also show 11, 10 and 7 as factors in the ratios, resp. 11^2 / 10^2 , then 35 / 33 , then 22 / 21, and finally octagon 77/75, with a circle area ratio of 9:10 , so the complementarity is everywhere, in these early prime-number relationships. ( The pentagon is approximate to the 9/thousandths, but just within the rules.)
(picture, the arcs)
The points in space that relate to each other are not in a rigid environment, it vibrates and bends, so the mathematics of their relationships are equal, but not so are the fields they are operating in.
This model ‘rationalizes’ the irrational square root of 2, which was Pythagoras’s nightmare, because the indefiniteness of the irrationality of square root 2 (V2) destroyed his belief in the integrity of number. Under Pythagoreans it remained a taboo to mention the subject. If only they had known there are these two primal ratios that form a completely consistent integrated whole as is shown in this work.
Irrational numbers are only valid in Euclidean space, but that does not exist one can argue, it’s an abstraction. All space is curved, not flat, space without matter is an idea, not a reality.
Space is the ultimate medium that materializes in fields of specific character (resonance-frequencies, their patterns and bonds).
(pictures)
The great advantage of this model is its pictoriality. The pictures ‘show’ the truth of the mathematical formulas as do the pictures of Euclid express a^2 + b^2 = c^2, in the positions of the pictured squares of 3, 4 and 5, as 9 + 16 = 25.
(pictures, see proof Pythagorean theorem, wiki)
You can see it before your eyes, the abstract proof is only in pictures, not numbers
Also the great pyramid is completely described by this model and is in a sense the most profound expression of it. (280/220= 1.618, golden mean).
(pictures, see proof Pythagorean theorem, wiki)
(picture, skeleton great pyramid, diamond)
The quintessence and intrinsic beauty of this model is expressed in my treasured emblem of this mathematics as the orange square of perimeter 9, inscribed in a blue circle of circumference 10. (it is here that established math gives a circumference of 9.0031.. for the square, so you know what we are talking about). So in terms of ratios here the side of the square as cord relates to the circular arc as 9 : 10, instead of 9.0031.. : 10. When we have accepted the priority of the natural 9 over the irrational 9.0031… then we can enjoy this journey along many familiar pictures and designs.
(picture emblem)
When we accept the new principle, we are forced to accept a new value for Pi (3.1415 926535 897...) (or short: 3.1416) in this relation, which turns out to be a universal factor for transforming any value with V2 into a natural number as circumference of a circle. This factor happens to be 2 x 10/9 x V2, or written 2.2222…V2, to be 3.14 26 9680…, the difference with Pi is 0.0010… , just 1/1000. This number happens to be the square root of 9.87654321, or 800/81 or 2^3.(10/9)^2 , which we will encounter later on. But mind, we now have entered the domain of the ratio 10:9!
In that respect I make the claim that Saturn’ s oblateness is geometrically a spindle torus with equatorial diameter of 10 and polar axis of 9 (120792:108325 = 10:9). This ratio exactly coincides with the geometry of the ring patterns of Saturn’s incredibly rigid equatorial field with its gaps and its wayward moons feeding on the rubble of the rings. (Saturn seems a late-comer)
But before we go there I must introduce you to another ratio which is crucial to our model, a ratio that was first calculated quite accurately by Archimedes who taught (c. 250BCE) that the value of Pi (ratio circum/diam) must be between 22/7 and 223/71. The latter value, 3.1408450…., is closest to canonic Pi (3.141592…) of the two, but we will concentrate on the 22/7 as = 3.14 28 57 1428…, because here we find the other primes we need, the 11 and 7 (2 x 11/ 7), next to 10 and 9 (2×5/3^2). These first 5 primes are, with 13, the foundation of this number logic. 13 also is part of the Pythagorean triangle, 5^2 + (3×4)^2 = 13^2 (again only the early primes involved here.)
Archimedes used polygons in his calculations for Pi, an, in principle, pictorial method. So also here the visible geometry is the decisive insight to ‘prove’ something valid. Polygons are central to the logic of this work and even some rare hypothesis on the nature of the polygons that they may be the 2-D representations of 3-D dynamics, like what might be the geometric basis of (cell) division, a , what I call ‘Siamese twin horn-torus’.
The octagon has a square root 2 relation to the area of its inscribed square. In this state there are 2 sqrts in one whole, eventually forming two simple square based horn-tori, which I call ‘core’-i (torus with core-point bordering the whole 3-D surface field, the corus, pl. cori).
(picture)
The sphere and the torus are supposed to be in this cosmology and ontology (metaphysics), the two representatives of the basic dynamics in the wave-geometry of space, they though are treated here as circles and squares to simplify the basic logic that sustains the dynamic. The natural numbers and their underlying geometric relations is what interests us here. A planetary orbit is a geometrical ring, a tube through which rolls a hurtling sphere, in resonance with the specific location created by the interplanetary resonance-field as a whole.
I cannot emphasize enough how much everything must be seen in a logical and organic whole
We can show that the numbers 9800 and 9801 are crucial in understanding division in nature mathematically, the 1 difference creates from 9801-1 = 9800, a double square area of 4900, the square of 70. The number 70 is 10 x 7 and one of those basic numbers we deal with only.
9801 happens to be the square of 99, another one of our pivotal numbers, which together make up our expression of sqrt2 in rational numbers, these are 99/70 and 140/99, resp. : 1.4142857… and 1.41414141… It depends on which denominator you need in the calculation/situation.
Every wholesome value (ratio) is predestined to have its function, whatever it is.
Mind you, a very beautiful rational approximation of sqrt.2 is 9801 + 9800 = 19601 over (2^2 x 3^2 x 5 x 7 x 11) = 13860 = 1.414 21356 4 213564 213564, that is 8 digits right and rational, that is enough to cover practically any curvature of space. And it involves again only the first 5 primes and nothing else.
The real great thing was recently that I could compress 24 years of work in 1 comprehensive geometrical picture with crucial numbers that sum up all basic relations in this geometry of space, easily on the side of a credit card
It is all about vibrating in certain standing waves, which makes it seem to be standing still but in reality it’s waves in resonance, vibration, all the time.