The Creation of Time

ATTENTION: This is a thorough revision and update of an earlier page. It is one of the most important pages of this website in which the fundamentals of the mathematical model and all the crucial archaeology is contained, but it is a work in progress.

Natural Number Logic and Geometry

                Analysis Third Pyramid in Royal Cubits

The scientific data on the megalithic works, translated into the mathematical measurement model here employed, together with the design of the works, form the keys to a natural-number logic and its geometry, which seem to have been understood and employed by the megalithic builders.
Although the model is basically simple as a toddler’s maths it is also confusing especially for those who are not used to mathematics anymore, so it may seem very tough still. It, though, nowhere goes beyond the most basic geometrical truths which most must remember from school and the model is a joy of simplicity and transparency once you know how it works. You don’t have to learn something new, only remember what you already know. The only numbers involved are 11, 10, 9, 8 and 7 and their multiples (esp. 14), so when Stone Age people could do it, why can’t you?

Here I give initially only the data which relate to the ratios of several of the most important stone circles in the British Isles and the design of three buildings. (Brodgar, Stenness, Maeshowe: all in Orkney; Stonehenge , Avebury in Wiltshire; Newgrange, Knowth in Ireland). The data reveal an underlying geometry of whole numbers and a recurring use of the same measures and ratios as has been shown elsewhere (see The Numbers).

Circle and Square

The most important fact is probably the discovery of the square by Neolithic man and its relation to the circle. This knowledge got immortalized in the design of Maeshowe. The present mathematical theorem is indeed, among many other things, about squaring the circle, but not by the usual area, but by circumference, which is quite a different story. ( a circle of circumference 40, becomes a square with sides 10)

The numerical ratios are based on four units of length which have definite ratios between themselves (see Bone Measures). To appreciate these ratios, like the differing values for Pi, one should notice that the same values are returning again and again, sometimes halved, sometimes doubled, sometimes quadrupled or more, in different units; this is what makes it confusing and where also I make sometimes mistakes. (I hope I have weeded them out now, but things are clearer, more visible in The Numbers). The aim is to show that all these (stone) circles in design are mathematically interrelated and that they themselves in fact express the basic ratios and principles of the geometries and of the logically consistent theorem, which is applied. It is not impossible that every stone circle by its size and number of stones expressed a notable date in the calendar. The counting of days could be done by marking a stone a day in the circle.
It is the Neolithic Cosmic Order, the Celestial Ratios, with the Rainbow Proportion at its heart that created the lay-out of the megalithic works.

Newgrange

The great Newgrange chamber, appears to stand on its own, and seems made up of triangles and a (skewed) hexagon, but is also much earlier than the others and possibly the spiritual source. The picture shows a solution to AB Powell’s (1994) observation that kerb-stone K-67 seems a lonely decorated stone, but this picture now also includes the decorated K-83 and K-84. Note that all these yellow lines are of exactly equal length, but this is probably ‘accidental’ in the eyes of our professionally ‘sceptic’ scientists.

Orkney

In Orkney we find mathematical and geometrical statements pur sang.

Maeshowe, just delivered

Most of the data here used come from A. Burl’s books on stone circles, if otherwise, the names are mentioned. In some cases there are no data, but these are then derived by measuring the official professional excavation plans, which always have scales, as with Stones of Stenness, or they are hypothetical design inferences as with the non existing bank of Brodgar and the height of Maes Howe.
The ditch of Brodgar has smoothly rounded edges where fixing a value is rather arbitrary, but my slightly broad value is perfectly defensible, I even think the rounded edges are deliberate, so as to include all the mathematical values of the theorem, without having to dig tons more of rock; the diameter of the platform edge value, 113.1m, is very close to the official data (Burl:113m) as is the middle of the moat, 122.52m (Burl: 123m) (see The number of Brodgar, 66?)

The Giza Pyramids

 

Given are also the values of the Egyptian Royal Cubit and the Remen of the Great Pyramid to point out the striking resemblances of the used units and the resulting geometries and to show that several key values of Brodgar are incorporated in two Giza Pyramids! (Brodgar is most probably earlier or contemporaneous. 2500BCE.) These will eventually be illustrated by pictograms.

Considering the often huge and rough building material, the ‘average’ nature of all data, the mix of feet and metre values, plus the rounding off in decimetres (Burl), I propose every value differing from the official data within 5 cm/2 inch in circles or 2cm/1 inch in buildings of over 100m, to be ‘exact’, whereas there are also differences caused by my consequent use of the Pi-factor: 22/7, which mathematically can exceed some 10 cm in big circumferences (Brodgar), but in reality are trivial because of the width of the stones; still most outcomes are much more precise, up to really ‘exact’.

The model is inherently imprecise, because it only uses whole numbers, but this evens out, as has been shown (Rationalizing the Ir-rational), differences of less than a thousandth are considered irrelevant due to the materials used or in connection with the tolerance of resonance; the theorem is logically totally consistent on the basis of its parameters, it are its practicality and ingenuity that stand out; it is a joy to work with because of its inherent transparency and beauty.

The following are the proposed standard values of measurement at the time, 5000 years ago, 3000 BCE:

Megalithic Ell ME= 0.52360m –Egypt Royal Cubit – 0.52375m (FlindersP.)
Megalithic Remen MR= 0.37025m –Egypt Remen –0.37035m (Fl.P)
Megalithic Yard MY= 0.82280m –A. Thom (MY) -0.8290m (=+6.2mm)
Megalithic Foot MF= 0.29620m –Roman Foot —–0.2962m (equal)

The Remen is taken as concept of a unit of length which has a square root 2 relation to a basic unit, in this case the Megalithic Ell, to overcome the ir-rationality of the length relationships.
The four standard units relate as follows:

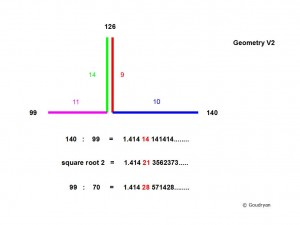
11 ME = 7 MY     ;     9 MY = 20 MR = 25 MF     ;     99 ME = 140 MR      (= 63 MY = 175 MF) 

Rainbow Proportion

 

Diameters Brodgar: 103.60m, Burl;   103.625m, Thom;  103.70m,  Renfrew;  103.67m Rainbow (mine, in between!)
It should be noticed here that A.Thom’s diameter is 125 MY, whereas mine  is 126 MY, because of the 6.2mm difference in the units. In the data for Stonehenge and other sites my MYard-unit length (.8228m) always fits better, even with regard to Thom’s own data, and produces mathematically meaningful numbers. 126 (=9×14)is the key to the mathematical model as is also shown in the height of the theoretical prototype, the 3rd Pyramid, 126 RC.(65.97m). Thom’s 125MY diameter has no meaning  (it’s a decimal system number) and does not render a circumference in whole numbers either, for yards, nor for rods, while 126 (because : x 22/7 = 396) does. Perimeter square 396 means sides of 99

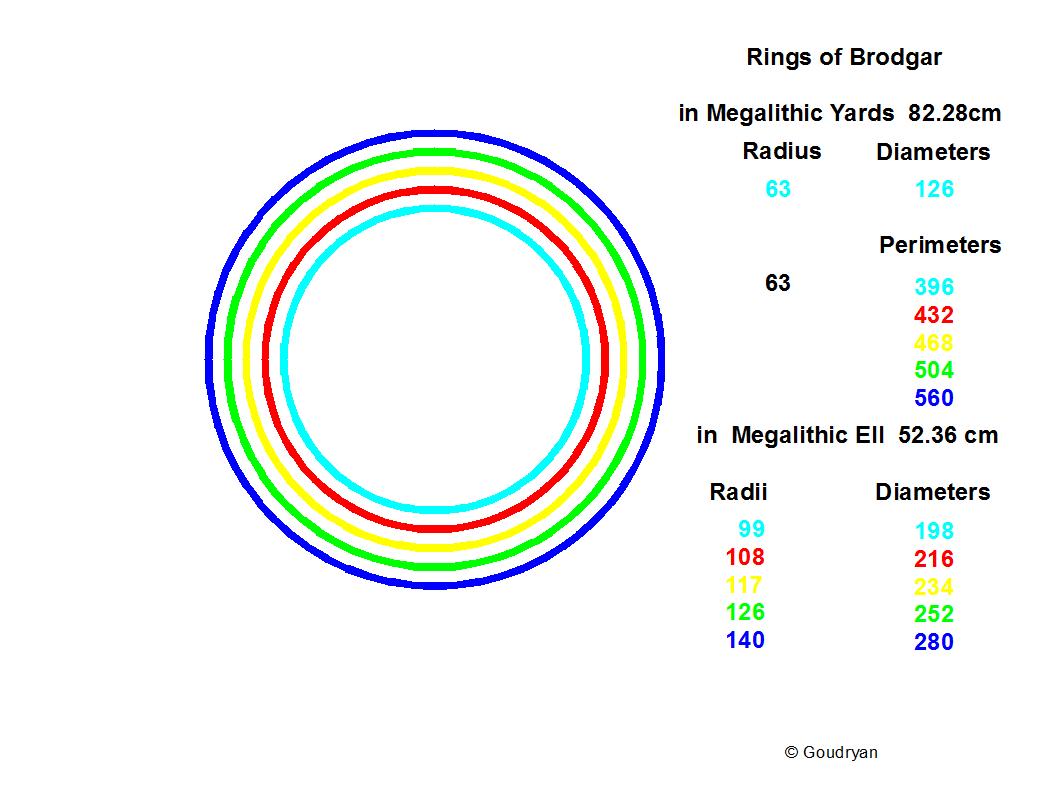
Rings of Brodgar :

 

Diameter stone circle (light blue)

126 MY = 126 x .82280 = 103.673 m
198 ME = 198 x .52360 = 103.673 m
280 MR = 280 x .37025 = 103.670 m
350 MF = 350 x .29620 = 103.670 m

Perimeter (light blue) :

396 MY— = 396 x .82280 = 325.829 m
880 MR—= 880 x .37025 = 325.820 m
1100 MF— = 1100 x .29620 = 325.820 m

Pi : 396 / 126 = 880 / 280 = 1100 / 350 = 22/7

Platform (red):

radius : 108 ME = 108 x .5236 = 56.549 m
diameter : 216 ME = 216 x .5236 = 113.10 m (Burl 113m)

Moat (red, yellow, green):

middle of the moat (yellow) diameter 234 ME = 234 x .5236 = 122.52 m (Burl 123.0 m)

outer radius : 126 ME = 126 x .5236 = 65.973 m
outer diameter : 252 ME = 252 x .5236 = 131.947 m
outer perimeter : 792 ME = 792 x .5236 = 414.691 m

The Rainbow Proportion here reveals itself in the ratio of the standing stones ring and the outer moat edge radii and diameters:

99 ME : 126 ME = 11 : 14
198 ME : 252 ME = 11 : 14

The most important aspect of Brodgar is that in its stone ring radius the four units are presented exactly where they come together in one length :
63 MY = 99 ME = 140 MR = 175 MF = 51.835m. (=100 Nippur Cubit! btw)
Twice this length (2 x 51.835) = 103.67m seems to be a crucial length.
The 103.67m I call the celestial length of the Megalithicum because it holds all classical units in integrals and doubles and appears everywhere in major megalithic buildings and sites.(Giza and British Isles)
It is the celestial standard of the Stone Age mathematical and cosmological model. The ratio resonance 63 : 99 : 140 : 175 .

Maes Howe, Orkney,   (2700 BCE,  about same time as Imhoteb, 2655-2600BCE at Saqqara, Egypt):

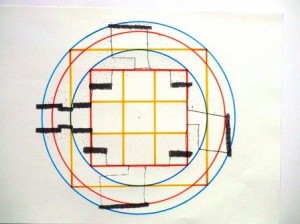
Data   A.S. Henshall:   Hall = 4.70m; Tallest upright = 2.95m; Passage 31ft = 9.45m; Cell height 3.5ft = 1.07m

Maes Howe design in my units:

Hall : 9 ME = 4.71 m
Tallest Upright : 8 MR = 2.96 m = 10 MF
Passage : 18 ME = 9.43 m
Cell height : 2 ME = 1.05 m
We see the differences are not over 2cm!

Diagonal buttresses : 8 ME = 4.19 m
Orig. height buttresses : 8 MR = 2.96 m = 10 MF
Between buttresses average : 8 MR = 2.96 m
Edges buttresses form cube : 8 MR = 2.96 m (8 is cube of 2)

Height roof (possibly) 9 MY = 7.41 m
equals : 20 MR = 7.41 m
also 25 MF = 7.41 m
or 14 ME = 7.33 m

Circle base square diameter : 18 MR = 6.66 m
perimeter : 40 ME = 20.94 m

Doubled circle diameter : 18 ME = 9.43 m
perimeter : 80 MR = 29.62 m
equals perimeter : 36 MY = 29.62 m
equals perimeter : 100 MF = 29.62 m

Double-Rainbow circle circumference : 72 MR = 26.66 m

Ratio ‘cell corner’-circles : 80 / 72 = 10 / 9

Ratio base circle to Double-Rainbow :    72 MR : 40 ME = 14 : 11

Rainbow Proportion : 9 MR : 5 ME = 14 : 11
(note here 9MR/5ME = 1.272 822…and 14/11= 1.272 727… which is within the accepted margin of a difference of a thousandth!, so treated as ‘equal’)

Maes Howe is not exactly square at floor level, which is due to the placement of the 4 ‘standing’ stones inside which indicate converging lines (intersection Barnhouse stone at 1/2 mile?), which may have been deemed more important than the exactness of the abstract cube, the roof construction though is definitely square immediately beyond the buttresses! It is supposed that a (rough) cube of 8 Megalithic Remen was indicated by the edges of the 4 buttress-standing stones and by the supposedly flat-topped buttresses, having the height of the tallest upright; the cube has a floor diagonal of 8 (cube of 2) Megalithic Ell between the buttresses (in reality only exact between East and West buttresses, because of the scewed lines, but still!).

Stones of Stenness :

Data Burl: diameter 31.70 m, moat width 5.80 m , bank width 6.40 m , platform diameter 45 m

S-Tones of Stenness (3300-2900) ?

The Stones of Stenness is an intriguing henge. Not only because it is probably one of the earliest henges, if not the earliest one, but more so because it uses huge flat thin vertical stone slabs of Orkney slate up to over 5m high, 3,5 are still standing and  impressively so, but the most phenomenal is the echo one creates yelling at one of the corners of the

I laser-measured 4 stones at 15.84m radius from one centre, SW-corner hearth, makes 31.68m diameter (Burl 31.70m), for half of the circle, this is exactly 77 Megalithic Tibia or 38.5 MY , the other half may be on a smaller circle, anyway 77 x 22/7 gives inner circumference of 242 MTibia = 121 MY (= 11 squared). Remember this regards the inner faces of the stones, when we add thickness more values emerge. They probably sought to incorporate as much information as possible, the spacing between the 12 stones, which is very regular, is then just over 10MY (121:12), whereas only 11 stones were eventually placed, it seems. (but the excavators may have missed one stone hole on a hair-breadth in excavation because it is on a smaller circle, not on an oval).
Stenness is a play with numbers and units, as in Maeshowe and Brodgar, we see the same numbers return in all, but also some new come in, like the prime 43 in 86. (43 is an eclipse number: 4×43+1=173, see Avebury’s Clockwork)

Circle diameter : 86 MR = 31.84 m (in standing stone body or outside stones smaller circle segment)

Platform diameter : 86 ME = 45.03 m (B=45m)     45.03 :  31.84 =  1.4142 587  =  sqrt.(2)

Moat width : 11 ME = 5.76 m (B=5.80m)
Moat outer diameter: 108 ME = 56.55 m (86 + 22= 108)

Midbank diameter : 126 ME = 65.97 m
perimeter: 396 ME = 207.35 m
equals MY perimeter : 252 MY = 207.35 m

Embankment diameter : 140 ME = 73. 30 m
equals MR diameter : 198 MR = 73.30 m

The last two values are: a conjecture (mid-bank) and a value derived from measuring the excavation plan (Richards).
The stone circle is not exactly concentric with the henge circles (see picture) and seems to have two centres, because at least 4 stones are on one perfect circle covering the west side of the ring with the other three within the margins, the east side (5 stones) could be on a different smaller circle, it is not an oval, but this seems deliberate possibly for acoustic reasons, it is though perfect in its spacing for 12 stones.
Stenness may have been designed specifically to produce certain echos (in winter?), it still has a definite echo in the centre, (mind you, with only 3 and a half stone standing; 5 thousand years the echos of the seething winds!) which may also have held for Brodgar (in summer?) where the spacing is irregular but the stone circle itself near perfect. The speed of sound changes with temperature, Stenness is optimal at minus -20C in winter, Brodgar at +25C in summer, so we have a winter and a summer circle, which relate well with the Moon and Sun circle folklore of Orkney.

Stonehenge

Next we come to Stonehenge one of the outstanding crown jewel of megalithic building  where we will see that crucial data from megalithic Orkney return in the sarsen ring and that the ratios again completely fit the model.

 

Diameter data: 29.60 m (Burl) ; 29.66m (97.33ft) Atkinson). According to Atkinson the circle is very accurate and the faces of the sarsens are tangent to it, with an error not bigger than 3 inches (7.5 cm)
Aubrey holes circle circumference : 271.6 m and diameter 86.39m both Burl and Thom. (done together?)
Overall site (incl. ditch width) diameter 110 m (Burl)

Inner diameter sarsen circle in our units is as follows in (MRemen=0.37025; MYard =0.8228 ; MEll=0.5236; MFoot= 0.2962)

————————————— 80 MR = 29.62 m
20 MR = 9 MY so 80MR = 36 MY = 29.62 m
4 MR = 5MF so 80MR = 100 MF = 29.62 m

Lintel ring inner diameter : 81 MR = 29.99 m ?
(this is unfortunately not the case, but may have been in the design, in practice it seems the lintels were adapted to the width of the available sarsens, see picture above, otherwise this would give the phenomenal ratio of 180ME circumference over 81MR diameter, which would be 20ME/9MR= Pi !!, here then Pi is Qute= 20V2/9)

Pi = 2 MY / 1 ME or 20 ME / 9 MR or 16ME / 9MF, so

Lintels inner perimeter: 180 ME = 94.24 m (180ME / 81MR = Pi)
180 ME / 30 lintel stones at 6 ME = 3.14 m each spacing centres sarsen stones
Lintels: inner arch length: 6 ME = 3.14 m (Atkinson’s average is 10.5 ft = 3.2m, but not taken along the arch, so 3.14 over the inner arch is at least close)
lintel arch width should theoretically be 2.5 MR = 0.923 m, but Atkinson gives an average of 3.5ft = 1.07m, so here is a problem, (though 2ME= 1.05m), on the other hand they had obviously no standard width (see picture). Thickness of lintel is 2 MR = 0.74 m ( Atkinson 2.5 ft = 0.76m)

The lintel ring’s inner arch nevertheless very closely approximates  the value of Pi as Qute in:

180 ME / 81 MR = 20 ME / 9 MR = 20V2 / 9 = Qute (3.142696…)
Sarsen thickness average is 3 MR = 1.11 m (data 1.10m)
Outer diameter sarsen circle : 86 MR = 31.84 m this is also an adequate value for the diameter  of the ring of Stenness! (Possibly the first henge ever to be constructed?)
Outer perimeter lintel ring : 270 MR = 99.97 m (270/30=9 MR), so for the outer arc of the lintels= 3.33m is the length of a segment, this is the radius of the circle circumscribing the ground square of Maeshowe, because the diameter of the square of 4.71m is 6.66m!

Note here A. Thom had 45 and 48 Meg. Rods for the inner and outer circumference of the lintel ring which is resp. 93.26m (mine 94.24m) and 99.48m (mine 99.97m) with diameters resp. 29.69m and 31.67m, which would result in a lintel width of 31.67-29.69= 1.98 divided by 2 is 99cm, which cannot be correct either, since the sarsens are 3-4ft (90-120cm) thick and the lintels match them. It seems the lintels have no standard width! This still does not say anthing about the original design, because that is what we are really interested in. The available material brought on the limitations! I hope though to find the clue in the measurements of the Orkney sites. Work in progress!

Inner diameter sarsen circle: 80MR=Perimeter Maes Howe outer cell circle = 29.62m
Outer diameter sarsen circle: 86MR=Diameter Stones of Stenness = 31.84m

Overall henge diameter : 210 ME = 109.96 m (Burl 110 m)
perimeter : 660 ME = 345.57 m = 420 MY
(660/55=12) 420/56 = 7.5 MY for spacing Aubrey holes via this circle
56 Aubrey holes perimeter : 330 MY = 271.52 m (B.271.6m)
Diameter Aubrey circle : 165 ME = 86.39 m = 105 MY (330/105=22/7 )
in ulna-bones  (MU)      : 330MU = 86.39
Radius Aubrey circle: 165MU = 43.20 m= 105 MT (Meg. Tibia = 1/2 MY )

Here my units exactly fit Thom’s own measurements, better than his yard or rod, (his prime 131 (rod) for the perimeter of Stonehenge has no mathematical or calendrical meaning whatsoever), the same holds for most other measures (Thom’s yard does not fit diameter nor inner perimeter of Stonehenge!) my units simply fit better and are always mathematically meaningful.

Ratio circles 330 MY : 420 MY = 11 : 14

Rainbow basic proportion (RBP) : 1 MY : 2 ME = 11 : 14
whereas
Pi = 2 MY : 1 ME = 22 : 7    !!!!!

RBP : Pi = 1 : 4

Qute: 180 ME : 81 MR = 20V2 : 9

Height lintel ring : 9 ME = 4.71 m (4.70) (=base square Maeshowe)
Height sarsen uprights : 5 MY = 4.11 m (4.10)
Width sarsen : 4 ME = 2.09 m (2.10)
Thickness sarsen : 3 MR = 1.11 m (1.10)
Height trilithons : 7.5MY = 6.17 m (6.10) = 15 MT
———-: 8 MY = 6.58 m (6.50)
———-: 14 ME = 7.33 m (7.30) ( original height Maeshowe)

To my great surprise I found in Burl’s standard work on stone circles (2000) a new and unexpected confirmation of the Megalithic Ell (ME) in the measurements of Newgrange by Powell ( Newgrange- Science or Symbolizm? 1994). Powell suggests a standard length of no less than circa 13.1 metres for Newgrange. c. 13.1m divided by 25 is c. 52.4 cm, which is the popularly cited length of the Egyptian Royal Cubit. (He is obviously not aware of this, neither is Burl). Expressed in Megalithic Ell it is 25 x .5236 = 13.09 metres!
Powell measured 6 x 13.1 = circa 78.6m from the chamber’s entrance to the opposite kerb stone 52, this is 150 ME = 78.54m, he further measured three times multiples of 5 and of 4 for his unit, which means 125 and 100 ME and one time each for 3, 2 and 1 of his unit, which is 75, 50 and 25 ME and once one half his unit which is 12.5 ME or 25 Megalithic Ulna (MU). But this was not all, he also claims that at Knowth a large measure of c. 11.10m was used, this is exactly 30 Megalithic Remen = 30 x .37025 = 11.1075m
What is astonishing about this is that the two units of measurement obviously seem to have been used in Ireland at a very early date and possibly came to Britain via Orkney (although no firm data are available for Orkney). It also suggests that the ultimate basic value is indeed the male ulna bone of 26.18 cm (male height 1.73m), this would multiply all the above values with 2, so we get 300, 250, 200, 150, 100, 50 and 25 ulna lengths in the design of Newgrange, which seems to employ triangles of the above ratios! The supposed close cultural relationship of the Maes Howe and Boyne Valley cultures seems ever more likely on the basis of the now available data.

Newgrange

Powell : 78.6m ; 65.5m; 52.4m; 39.3m; 26.2m; 13.1m; 6.55m

In Megalithic Ell this is resp. —— 150 ME = 78.54m = 300 MU
doubled in Megalithic Ulna ——– 125 ME = 65.45m = 250 MU
(MU) —– 100 ME = 52.36m = 200 MU
75 ME = 39.27m = 150 MU
50 ME = 26.18m = 100 MU
25 ME = 13.09m = 50 MU
12.5ME = 6.55m = 25 MU

Knowth

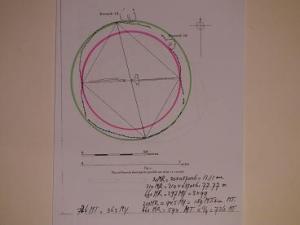
Note here the Rainbow proportion, red-green, 11:14

Knowth would have been set out in (female) fibula units of 30 x .37025 = 11.11m in my view, whereas according to AB Powell it is an 11.10m standard measure. The picture shows again in analysis a Rainbow proportion, here in the triangles that make up the inner lozenge.

*******

Brodgar and the Pyramids

The diameter of Brodgar as 103.6 m – 103.7 m ( 103.67m = 198 ME =126MY=280MR=350MF) has been assigned by several top-surveyors at some point in time it has been assigned to the south (and north) inner stone circle(s) of Avebury and even to the (irregular) stone circle around Newgrange in Ireland, it can also be found in the oval moat of Maeshowe (103m; or 35cm more on each side)

The Rainbow diameter value is 103.67 m , this value (knock off 1 cm) multiplied by square root 2 gives the height of the Great Pyramid : 103.66 x sqrt(2) = 146.59 m (Lehner), thus the circumference of Brodgar, which is 880 MR, 325.83m, therefore equals the diagonal of the Great Pyramid (Pi), which is also 880 (Egyptian) Remen = 325.78m. (Cole diagonal data: NE-SW= 325.699; NW-SE=325.868; average : 325.784m) This is because the same mathematics is used and practically the same unit of length. ( The Ludwig Borchardt/Cole Royal Cubit of 52.355cm / Remen of 37.021cm fits the Great Pyramid best (Cole: average base side 230.364m /440 RC = 0.52355) and comes closest to the Megalithic Ell; it is therefore used here to get the best fit)

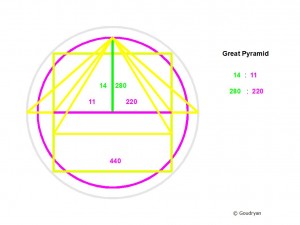
The design data even fit better the Third Pyramid (Mycerinus/Menkaure) which is here believed to have sagged a bit, because of inferior construction, but is meant to be the mathematical key to the Great Pyramid ratios, height is 126 RC = 65.97 m = 126 ME (65-66m, Lehner) = radius of Brodgar moat; the diagonal is  280ME = 396 MR = 146.60 m,(= height Gr. Pyramid, don’t bother the centimetres!!), the side of Menkaure would be 198 RC = 103.66 m , at east-platform level, which is the diameter of Brodgar.
Lehner’s data (102.2 m and 104.6 m, average 103.4 m ) are dubious here because they imply a rectangular instead of a square base for the pyramid which would be highly unusual; the Rainbow data (103.67m) are about the average of Lehner’s. (diff. 27 cm; his sloppy measures for the Great Pyramid sides (all 230.33m), can never add up to a pyramid combined with his other data, this is not helpful either)
Another strong argument for the height of 126 RC for the Third Pyramid is the height of the Second Pyramid at 274 RC = 143.453 m (Lehner 143.50m), since 274 + 126 = 400 RC, whereas  Thom’s 125RC would make 399 RC, a meaningless number.
The key to the Second Pyramid (Pythagoras!) is the prime 137, because the height is 2 x 137 = 274 RC, whereas the side of this pyramid is 3 x 137 = 411 RC = 215.18m (Lehner=215m, Fl.Petrie mean=215.26, north side 215.19m) (Lehner’s data often lack the precision of earlier surveyors, later measurements are not necessarily better, so I feel free to use those data which fit my model best)
The height of the Second Pyramid, 274 RC, this is 2 x 250V2 – 250V3 = 707.1.. – 433.0… = 274.09 ( x 0.52355 = 143.50!, Lehner), 250 RC is the parallel distance between Great and Second Pyramid. (For lay-out and many other things see the great work done by John Legon).

Probably the best argument for the 198ME side and 126ME height of Menkaure is the distance from the King’s chamber floor to the top of the Great Pyramid at 198ME and the level of the air-channel exits at 126ME under the top, the height of Menkaure!, which indicate outside the sides of the Great Pyramid of again 198RC at that level, equal to the side of the Third.
The Third Pyramid is a replica of the top of the Great Pyramid and its prototype theorem.

According to our model, the volume of the Third Pyramid is ‘exactly’ 1/11 of the Great Pyramid (diff. 0.025), so the Menkaure-top of the Pyramid has a ratio 1 : 10 with the rest of the Pyramid and a ratio 1 : 11 with the whole, a perfect scale, stressing another time the importance of the number 11 in the design.
The revealed ratios are now (400= 274+126 and 280=Great Pyramid) :
400 : 280 =  10:7
280 : 126  =  20:9
280 : 274  =  140:137
274 : 126   =  137:63

I will show all this in pictograms in due time.

Copyright 2009 Yan Goudryan