The Creation of Time

The Ell and the Yard

  

Contrary to the prevailing archaeological paradigm of the cult of the dead, ancestor worship and all the priests, ritual landscapes and ceremonies that come with it, I start from the practical and the useful, because that is what people occupies most of the time. The cult aspects are presented by archaeologists as the leading motives in megalithic culture; the words and concepts employed in this cult paradigm always carry hierarchical and cultural connotations which are foreign to the developing egalitarian society, which the late Stone Age culture was. To a certain extend before this period there was no society as such.

Retaining bones of the dead, we know, was widespread in Mesolithic Europe, it was a domestic issue, so people carried bones of their relatives with them and kept them in their temporary dwellings. These bones had no doubt great significance for them in relating to the dead, whatever form that took on an individual or collective basis. They may have been good luck charms and ‘souvenirs’, or guardians, but the care for the bones by all means expressed a care for the dead, not a dread for the dead (as in cultures where the dead were taken away from the living to isolated places, islands).

In early Christian Ireland bones of (supposedly) holy men were traded by monks, not a Christian inspired custom one would say, but no doubt catering to a demand by the population, which had its roots in very old traditions and beliefs regarding bones of holy men (or old ancestry). In many religions today bone relics still have this aura of magical power and sacredness, so there is nothing particularly alien or primitive about such care for bones. It is very understandable, but the collective and egalitarian character of interment of bones of the megalithic culture is remarkable. That is also the big difference with the emerging Ego-era of the ‘Beaker people’ that followed; individual burial would become the norm, till today.

What we can see in the late Stone Age is the emergence of collective works and how these became focal points for the formation of communities. The first of these focal points may have been to build a communal burial mount as a place where you could always find back your buried relative. Dramas may have existed with people unable to find back the place where they buried their loved ones a year earlier. Humans for the first time were really discovering they were capable of improving their long term everyday life in a communal effort, which created works in sizes never made before, works with a lasting benefit.

This may in the megalithic culture eventually have led to a posturing for status by building ever bigger sites, or using ever bigger capstones, but at least the major collective early works turn out to have been ruled by mathematical principles in their design and needed their size to express their mathematical content. This strongly suggests that the act of building mathematically itself was either considered auspicious or was the very aim of the design, or both, in any case it would bring harmony to the design and to the space defined by the design; it would preserve a mathematical truth which could be understood as a heavenly principle, with the key of the mathematical logic hidden in the design. This key is in the design of Brodgar, of Maes Howe, of Stonehenge, but also of the Giza pyramids, they are all the physical embodiment of mathematical truths, and in this case even a related mathematical truth.

To build these major works measurements had to be made and units of length be communicated. Through experience and logical thinking a system of standard measures and whole number logic would have come into being. It is because they had these measures and their skills that they could build these large collective works. All standard units of measurement are traditionally related to the human body, palm, finger, foot, thumb, ell (-bow).

In my view certain types of the collected bones came to be used as standards of measurement, which would explain the striking uniformity of measurements in major buildings all over the British Isles as has been shown elsewhere (Metrology 1&2), with regard to some of these buildings and circles.
On the basis of a mathematical analysis of megalithic measures, I have come to the conclusion that megalithic man used three, maybe four, types of bones in his measurements, which related to each other in a particular mathematical order; the bones were: the ulna, the fibula and the tibia, possibly the humerus (upper arm), respectively forearm, calf and shin bones.

These bones were chosen for a specific standard length and could not derive from the same skeleton. The root unit would have been the male ulna with a length of 26.18cm, which corresponds to a male body height of 1.73m, an average in Neolithic times.
Slightly longer bones could be filed back to the desired standard length. The corresponding fibula of 37.025cm would come from an adult female skeleton or a young male, the tibia of 41.14cm again from an adult male. (humerus=29.62cm)
Two of these bones, the ulna and the tibia would have been doubled to form standard ‘scientific’ units, respectively the Megalithic Ell (ME) and the Megalithic Yard (MY), the fibula would have been the Megalithic Remen (MR)
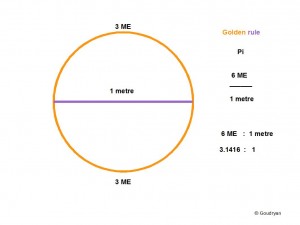
The precision I suggest with these precise values are for the sake of the mathematical model. But because the value .5236 (ME) times 6 is 3.1416 which is virtually canonical Pi (3.14159….), it is an ideal value for practical reasons, then, for every metre in your measured diameter you can immediately calculate the amount of megalithic ell (ME) in the circumference by multiplying by 6 and see how it relates to the number of stones, or the other units of measurement.

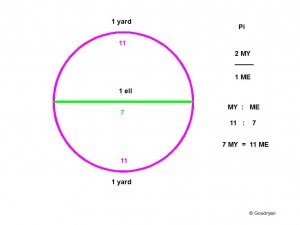
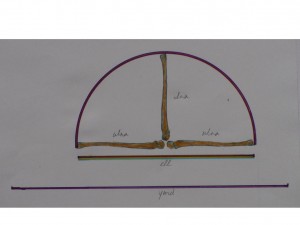
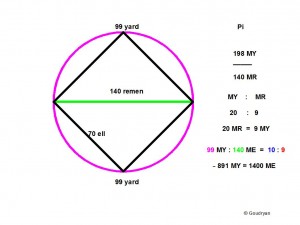
The word ell is derived from the Latin word ulna, and the word el-bow, no doubt, from the 180 degree arc the ulna can make by the elbow joint, this would then be the basis of two ulna in the standard unit of one Ell, being 52.36cm. (see picture). To overcome the problems of the incompatibility of radius/diameter and the full arc, a new unit of length was created, the Megalithic Yard, which had the length of the full elbow-arc. Instead of an ir-rational, even ‘transcendental’ number Pi, their Pi would be a simple 2 Megalithic Yards over 1 Megalithic Ell. In formula Stone Age Pi = 2MY/1ME.

Once they stretched the arc straight they would find that two appropriate tibia bones fitted the length exactly, so the tibia became the root length of the Megalithic Yard. The next step was a unit which exactly fitted the incompatible length between the tips of the perpendicular ulna bones, and this was the female fibula. This way Stone Age man solved the practical problems of the incompatible lengths which are involved in this fundamental mathematical scheme of diameter, square and circle. (This new MY is derived from the circumference, while Alexander Thom found it as a statistic average from stone circle diameters,and doubled the outcome to a handy yard-like measure.
I have no explanation for this, but my slightly smaller value (-6.2 mm), that is 82.28cm as opposed to Thom’s 82.9cm, always fits the data better and more meaningful and is in no need of a Megalithic Rod of 2.5 M.Yards = 2.0725m as Thom used, to accomodate the problems encountered with his yard length, it did not fit).

This then results in the following ratio interconnections between the bones and the different lengths.

ulna:tibia    = 7:11
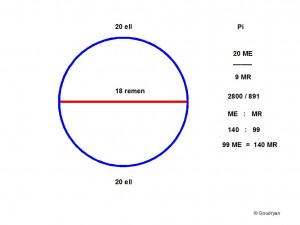
tibia:fibula = 10: 9
ulna:fibula = 70:99

ell:yard          = 70:110
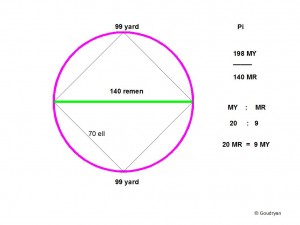
yard:remen = 220: 99
ell:remen     = 140: 99

In the following pictograms I make clear how the different unit lengths hang together; it is so simple that it is confusing.

In my view the megalithic yard derives from the megalithic ell in the the way the picture shows.

The use of two different units, differing in the required ratio, is the practical solution. It is a perfect way of expressing Pi in whole numbers and evade incompatibility.
2MY / 1ME

Here we find a slightly different Pi which corresponds to a fourteen over eleven (14/11) situation, but still made of the same numbers. The Remen here is set against the Ell. So this is the other rational value for Pi we employ.
20ME / 9MR

We find the two values when we substitute square root 2 in the formula of Qute (20/9 V2) by 140/99 and 99/70.

Here we see how Pi can also be expressed in Megalithic Yard and Remen, it is 99MY over 70MR, or more properly 396MY over 280MR.
396x . 8228 = 325.8 m over 280x . 3703 = 103.7 m  = 3,14 17 55…  (Pi = 3.14 15 9….)

This is the exact formula and measure of the stone circle of Brodgar. It shows all the aspects of the theorem in whole numbers.

99MY / 70MR

This is the simplest way of expressing how the three units interrelate. Because it are constantly the same ratios in different units, it can be confusing, but it is a joy to see how everything hangs together in an unshakable logic.

This aspect of the exact value I give for the Megalithic Ell (0.5236m) I hope will secure the use of this model quite soon, that is that 6 ME are 3.1416 metres, which is the value of Pi, this means that for every metre in the  diameter there are 6 Ell in the circumference.
6ME / 1Metre

So if you have 110 metres as diameter of the ditch outer perimeter, as at Stonehenge, then you have 6×110 = 660 ME circumference and (660/22) x 7 = 210 ME diameter.( 210 x .5236 = 109.96m ~ 11om)

But also (660/11) x 7 gives 420 MY which can be divided by 56 (Aubrey holes) and gives 7,5 MY or 15 Tibia, that is 15 x .4114 = 6.17m spacing in the big circle to set out the centres of the holes in that smaller Aubrey circle.

 

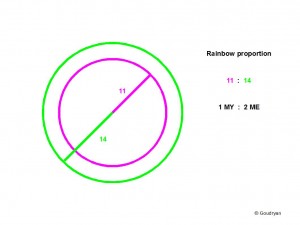
Last but not least we find in the Rainbow Proportion the mirror value of Pi. Whereas ‘megalithic’ Pi is 2MY over 1ME = 2MY/1ME,
the Rainbow is:
2ME / 1MY   or
(2×7)/  11   =    14 : 11
This ratio is of intrinsic beauty because   (14/11)^2 = 1.6198, very close to golden section 1.618…  and even closer to 1.62, which is the ‘stone age’ section, it is the square of  0.9V2, the diagonal of  0.9^2.

We see here how this is all intricately connected, which may make it confusing, but it is in fact straightforward and simple in principle. (When you use a calculator and put the values in you will see that it fits, the confusion stems from the values reflecting the ratios which make it appear contradictory in formulas)

I appreciate that people will find it extremely hard to believe that Stone Age man would have known the mathematics I claim he has known. But our disbelief stems mainly from our own struggle with mathematics and because we hardly know anything about the night sky ourselves. Would then that be the standard we measure by, that is, our own, in some ways embarrassingly limited, knowledge of the world around us? They definitely knew more about that than we do and in different ways. The bridge is the mathematics. I have no reason to think they could not have found out what I did as an ‘ignoramus’ myself. Once you have the ingredients the system is very clear. The accumulated knowledge was taught by repetition and by drawings in the sand. These would be the first schools to preserve the ‘Known’, the first genuine civilisation.

We can see the model is not difficult, it is clever, maybe confusing, but not intrinsically difficult, so why would they not have come up with it? It is there for anyone to find in principle, as I have shown. They were definitely occupied with circles and in Maeshowe with immortalizing the discovery of the ‘Square’ and the ‘Cube’ and probably the Rhythm of earthly and cosmic time cycles.

*******