The Creation of Time

 

17/11/2011

Maeshowe in winter snow, winter-solstice

Intro

This is a kind of work-out of Metrology in the Neolithic (Metrology 1) because it definitely confirms the intention of making the length of Maeshowe’s buttresses diagonal of 8 M.Ell (4.19m) recur in the design so as to emphasize its significance. Here we see the anatomy of the design and reveal the amazing network of triangles and preferred lengths.
Pictogram 1

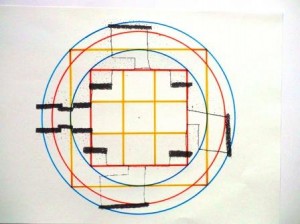Maeshowe design, Celestial proportion based on square-9, sphere & torus (resonance)

The Cube in Maeshowe

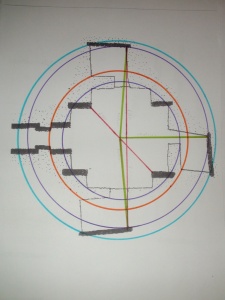
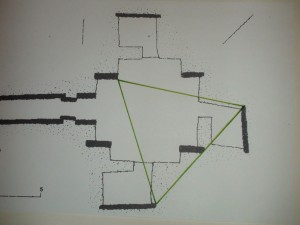
I found the following among my many unpublished pieces. It is a forgotten but fresh confirmation that the cube I envisage between the buttresses of Maeshowe, which must have a diagonal of 8 M.Ell, and sides of 8MRemen= 10 MFeet, indeed is sustained by the distance of the back-corners of the left- and right-hand side cells to the axis of the building, here horizontal (see picture below), an axis which goes through the middle of the passage, the centre of the chamber and exactly passes through the left-back-corner of the back cell, all on one (purple) circle. Note the angle of that back cell-wall, here at right-hand side, even narrowing the entrance to the cell. Ideally the sun at the winter-solstice slides along that cell side-wall to the back-corner, the exact axis.
Pictogram 2

red lines equal 8 Ell

In the early stages of this archaeological investigation I had access to Maeshowe with a guide to make my own laser-measurements, from these measurements and the data for Brodgar I concluded they used practically the same units of length as the Egyptians, the Royal Cubit and Remen, but probably earlier and that they also employed the same whole number geometry and even that they based their architecture on a square of 9 Megalithic Ell (4.71m), the relation of circle and square, sphere and torus, the heart of the mathematical model I have developed. This may sound incredible but it is sustained by the facts, which are amazing enough also without the Egyptian connection. (In the first diagram the laws of sphere and torus resonance are contained as I show elsewhere on this website, this you might also not have expected in this context, but I do not claim they knew this, it is just in the geometry, the resonance is my inference.)

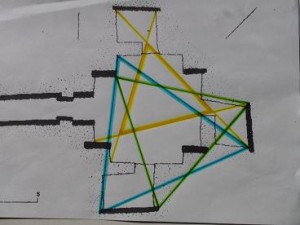
Maeshowe equilateral triangles

Rainbow-radius Maeshowe
For a second time I was granted access to Maeshowe for measurements and this time I measured the crucial distance in my theory of the entrance-back-corners of the left and right hand side cells (Pictogram 2 upper and lower) to the exact centre of the chamber as this signifies the radius (green lines) of the double rainbow (purple circle) according to the math model. In my theory the radius of the double rainbow should be 4.24m., when based on a square of 9ME = 4.71m (square root (4.71^2 x 2) = 6.66 then divided by 11/7 = 4.23 8m. (4.238 : 3.33 = 14 : 11 = Rainbow Proportion) This distance would ideally regard the faces of the back-slabs in the cells, the corners proper. Would I be confirmed was the question.

Maeshowe cube-square

Laser
With the laser I found the following readings of 4.27 8 (NW), 4.23 6 (NE) and 4.21 7 (SE) = 4.24 3 average, this makes a diameter of 8.48 6m, which was a very good result indeed given what was inferred from the design: 4.24m and the margin of the ‘exactness’ of the centre I took my measurements from. This finding was sustained by a later visit and reading of the direct distance of the opposite corners of the right and left hand side cells. This distance was 8.36m, which is 2 x 4.18, this being virtually 8 Megalithic Ell (4.19 m), exactly the ground-square diagonal of the projected cube between the buttresses, so twice this distance, 16ME (8.38m) is slightly shorter than twice the radius of 4.24m (=8.48m) because it does not pass through the centre of Maeshowe, but is just off-centre by ~65cm.
The beauty here is of course the cube numbers 8 and 16 as powers of 2 and as 1 and 2 cubes volumes which appear here to emphasize the importance of this number and this particular distance, that is, the 8 Ell diameter between the buttresses. This distance is actually existing in Maeshowe because although there is no exact square between the edges of the buttresses, still the lengths between them is: 3.05^2+ 2,87^2= 17.54 of which the root is 4.19m being exactly 8 MEll, which is in fact to be found between the East- and West-buttresses. The number 8 here is important because it is related to the number 9 of the ground-square, the numbers 8 and 9 we find also squared as 64 and 81 in Vedic temples so it might be we see here archaetypical Indo-European roots in temple building. One could argue that Maeshowe with its open roof must have been one of the first, if not the first stone building worthy of that name: ‘temple’, ‘Pantheon’, but not so much in a ‘religious’ sense but ‘cosmological’ that is ‘scientific’, with an open window on the night sky. A temple of science, like the early pyramids, but also there it was in fact all ‘One’ .

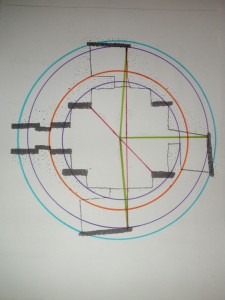
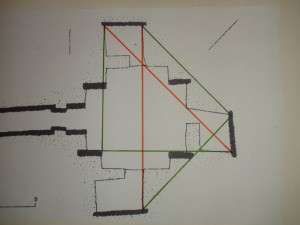
Maeshowe design: 3 green lines are radii from centre, 3 red lines are 8 M.Ell, the diagonal size.

Some circles here have slightly different centres, like at the Stones of Stenness nearby, but remember this is a drawing of 1946, while my measurements are reality and closer than the drawing suggests. Having measured a laser scan of Maeshowe (see below), it appears everything is confirmed, even the anomaly of NW-cell, which though enables the full unobstructed stretch of the crucial 2x 8 Ell. Note what a subtle design with the red lines holding the number 8, just off-centre, but ending on the purple circle, the double (second) rainbow. Maeshowe is most subtle of all Atlantic megalithic buildings, it is the quintessence of the mathematics of the squaring of the circle by perimeter, producing the ‘Rainbow Proportion’ (11:14) within the ‘Celestial Proportion’ of the overall design.(Pictogram 1)

The state of archaeology.

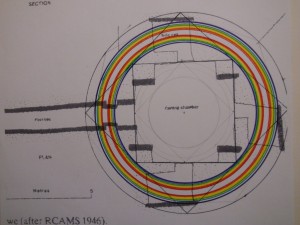
Because of the nearing winterstolstice I had another look at the lay-out of Maeshowe, and found more confirmation for my bone-length system than I ever could have hoped for. On top of that I found a recent laser scan of Maeshowe which confirmed a slight inaccuracy of the plan of 1946, which was the only one there was, as far as I know. Although the scan is an improvement it is still not good enough in detail to do the proper job (the lines are too blurred) but at least now I know that the NW-cell (left of passage, which itself has SW-axis) is indeed nearly rectangular, but the back-cell as well, and it is slightly deeper than on the map. I am forcing the picture here, this has to do with the inaccuracy of the 1946 RCAMS-plan. So lets make a fresh analysis with the now available information and the new discoveries I made.

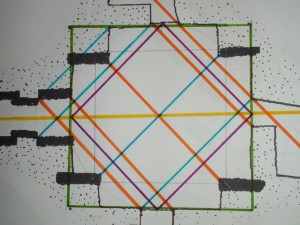
In the chapter the Rainbow Proportion I show the circles and squares which form the mathematical theorem I had found years ago and apparently the design of Maeshowe is based on. Another close look at this design where squares, rhombs and parallels are the keys, reveals a striking new confirmation of the care which was taken to express the mathematical intentions and we get a rare insight in the way they set this whole thing out, initially. In the Rainbow picture (above) we see the large rhomb (in vague black lines, side 18 Remen) as the double (area) of the ground-square, 9MEll, which itself is circled by the inner rainbow and has again an inscribed rhomb (side 9 Remen) as half area of itself, which we see return as square on top of the buttresses where the square roof corbeling has narrowed to this proportion (half the ground-square in surface!) (read below); the 11:14 ratio is in the double-rainbow proportion, where the second (purple) circle, touching the back corners of the cells equals the perimeter of the large square (4×18=72Remen), the double of the ground-square in surface; this is the heart of the theorem. It is indeed all about squaring the circle by perimeter, not surface. The ground-square defines the first rainbow circle through its corners (40ME) , the second, the double rainbow is then defined by the circle with circumference equal to the perimeter of the doubled ground square (large rhomb) (72MRemen) (72/√2 : 40 = 14 : 11)

Maeshowe corner parallels When we see the perfect perpendicular grid arising from connecting the many corners of Maeshowe we can also see that there was method in the deviation from the confines of the original geometric design. What we see is that the main diagonals between the buttresses are exactly perpendicular without producing a square. The N-S diagonal is longer, the south stone (left lower corner) is set deeper into the wall, to preserve the perpendicular! Obvious is also that the alignment of the standing buttress stones is not parallel, but probably focused on the Barnhouse stone, half a mile away, 1000 MYard=823m. The axis is also perfect as the picture shows.

Great was the delight when it turned out the longest red line through two side cells, exactly cut in half by the blue diagonal, is the same as the earlier found distance between the back-walls of the opposite cells (see above), that is the 16 Megalithic Ell (8.38m), so that both halves are equal to the distance between East and West buttress, the important 8 MEll red diagonal (4.19). The buttresses point to the cardinals and are exactly North, East, South and West, which may have been the reason for the perpendicularity being preserved in a bit a skewed, lay-out. We will see that it seems that for them specific standard lengths were more important to be incorporated than an exact fit of the original mathematical lay-out of the theorem. It seems as if, with the base of the lay-out a perfect theorem, the Celestial Proportion, they tried to incorporate more sustaining, yes, explanatory information in emphasizing certain lengths. (In the 1946 picture it is not the same length but the scan shows it is correct within centimeters if not exact. See how even the entrance of the NW cell is widened to accommodate the -unobstructed- line! This is another undeniable confirmation of the importance attached to revealing the 8 and 16 Megalithic Ell lengths and other lengths, forming the ratios (more will follow).

Maeshowe design corner connections, each colour stake has the same length!

We see this ‘sticking to specific lengths’ in the many ways this was done, which show in the different pictures. Here we see that the yellow, green and purple lines indicate each such a specific length.

Maeshowe corner-connections

Another picture with only green lines shows an enormous amount of one same distance between outstanding points in the design, here it is the suddenly occurring length of exactly 16 Megalithic Remen, being 2 x 2.96 = 5.92m, the green lines, where 8MR= 2.96m is the (averaged) distance between the buttresses and supposed to be the side of the envisaged cube. Below we will see how this 16MR occurs here no less than 10 times and is embedded in Pythagorean and equilateral triangles as well.

The length of 16 Megalithic Remen

The following pictures show how this green length of 16 MRemen relates to the already found length of (2×8=) 16 Megalithic Ell, the orange line. We see here two identical Pythagorean triangles, both with hypotenuse (orange) of 16MEll, and both with the above mentioned 16MRemen (green) forming the two right-angled isosceles triangles. This is the best proof I could wish for regarding my contention that they had these different units of length relating as a ratio with square root 2, that is 1MEll : 1MRemen as √2 : 1. QED.

Note the exactly parallel lines!

We find another equilateral triangle of this measure of 16MRemen which makes this now occur no less than 17 times in the lay-out (possibly more), it is clear this was an important ritual length to them.

Equilateral triangle This equilateral triangle of 16 MRemen is another confirmation of this crucial length. This whole pictorial analysis cannot but amaze us by the consequent use of this length. Again and again we see these connecting lines not only connect but also often touch on or going parallel with other aspects of the design. What we can begin to unravel with this analysis is their way of going about a design, because all I point out here must be seen as belonging to the earliest stages of the building, a lay-out on a clay platform where lines can be drawn but also easily erased. Maybe they have spent years working on the design to get as much information in as they could and to fully exploit the amazing versatility of the theorem and their design. Certain is that the buttress-standing stones, are not real standing stones because they don’t stand on their own, they need some incorporation in the wall to stand since they are hardly dug into the ground, less than 30cm. Nevertheless they would already have been placed when the first contours of the square walls were raised in stone.

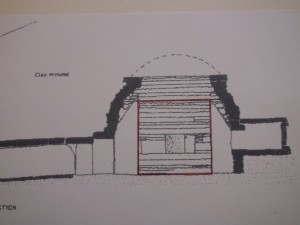
We see here close-up the tops of the buttresses as pictured in 1861, with my envisaged type restauration, level with the top of the east buttress, unlike the ugly ‘restauration’ of today. As far as I can make out on these pictures the ‘square’ at that height over the buttresses of 2.96m is exactly 9 Megalithic Remen, which is the square-rhombus in the basic square of 9 Megalithic Ell, as 9ME is indeed √2-times 9 Megalithic Remen, by definition. This means that on top of the buttresses could be placed four lintels of 1/2 Remen (18.5cm) width to realize a stone lintel- square on top of the buttresses with outside measure 9ME (3.33m), conform the roof-square at that height and an inside measure of 8MR(2.96m), which would then with the edges of the buttresses form the cube with inner dimensions of 8 MRemen= 2.96m cubed, as argued all along. QED. (It would in no way be perfect, but should it? We do not know why the ‘standing stones’ of the buttresses are aligned as they are, there is little in the way of ‘mistakes’ in the rest of the geometric design)

Maeshowe design: purple square of 9Remen in the green base square 9ME, equal to the (vague) black square on buttresses, the contour of the corbeled roof at that height.

Analysis design Maeshowe

It is again more than rewarding to scrutinize the lay-out of Maeshowe and it shows the incredible sophistication of the design, the playful use of again and again the same lengths and the significance of these lengths of which the 16 MR relating directly to 8ME are now familiar, 9 Remen relating to the basic 9MEll, but also other repeated lengths are significant, all that has to wait until ever there is going to be a really proper lay-out in scan and on paper of this historic design, but since understanding Maeshowe is absolutely no priority in archaeology (it’s a passed station for them, no headlines to be grabbed), this can take a long time. This building is in a sense no pre-history anymore because here knowledge is recorded in the language of numbers, of mathematics. A statement is made, a definite message related: – ‘this is what we know’ – and it can be understood, by us, now, 5000 years later, that is reason for great joy and profound wonder. Not for archaeologists, though.

Conclusion

So again we have been able to extract a lot of information from the design of this magnificent Neolithic building, which is based on mathematical harmonies and symmetries. I cannot emphasize enough how important the parallels and symmetries are in the design of Maeshowe, a typical fruit of the discovery of the square and its relation to the circle, the diagonal as diameter, the square in the circle in the square in the circle, the factor 2 involved………ad infinitum. The awareness of parallels and impeccable straight lines, yes, of the square itself, unique to Orkney, most probably stems from the natural occurence of parallels in Orkney’s sandstone formations that are a natural geometry and became the inspiration of an ‘unparallelled’ culture of mathematics and abstract thinking. In those halcyon days Nature taught people its lessons because they still listened and knew how to listen (shaman, druids later), today scientists think they can teach Nature a lesson, but IT doesn’t listen, IT hits back.

What is preserved in Maeshowe, and Structure-1 at the Ness of Brodgar, were momentous findings and pieces of pristine new knowledge of the late Stone Age, which our Stone Age scientists and cosmologists sought to preserve and immortalize in stone, ‘forever’, as a mystic bond with the universe and posterity. Is not that an hommage to those Giants that went before us, on the shoulders of whom we stand as Newton put it.

It took ‘only’ 5000 years to be recognized.

********

Another proof (12/4/12)

Maeshowe: Identical Pythagorean and equilateral triangles in design

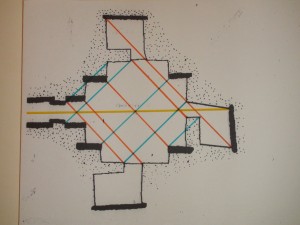
(This is a later insert on the metrology featuring the scan)

The ‘space-probes’ are scans of the stone work inside the mount of Maeshowe. Measurement of the scan is an even stronger confirmation of the two parellel aligned rectangular (Pythagorean) triangles (a²+b²=c²), than in the 1946 black bar design (above, lower), also the equilateral triangle (orange, yellow) is clear; all these lengths are equal. Since we know the blue (green) lines to be 16 Megalithic Ell (8.38m) – this is twice the distance 8ME (4.19m) between East and West buttresses – this means the orange lines are 16 Megalithic Remen (5.92m), since ME : MR = √2 : 1. Is there better proof that they were aware of the ‘incompatible’, lengths of √2 and 1 and devised different units?
Like others, they used different units to preserve whole numbers, like the cubit and the remen in Egypt, but here even more can be derived like the megalithic yard and foot. These units follow from the approximate whole number proportions of circle and square, where the ‘irrational’ diagonal of the square at the same time is the diameter of the encompassing circle. Unraveling this Gordian knot in whole numbers is what I have done on this website (Bone Measures etc.) and what I claim they had done before me and had put, by means of the crucial ratios, into the designs of their buildings.