The Rainbow Proportion
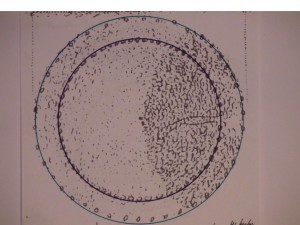
 During this summer (2009) I realized that the model I have worked on for over ten years now, holds the double rainbow proportion, which is the fixed proportion of the diameters (radii) of the two rainbows that constitute the double rainbow, being 11 : 14.
During this summer (2009) I realized that the model I have worked on for over ten years now, holds the double rainbow proportion, which is the fixed proportion of the diameters (radii) of the two rainbows that constitute the double rainbow, being 11 : 14.
(Inner lilac circle : turqoise circle, see picture).
It is true that this proportion cannot be strictly defined because of the vagueness of the rainbow edges and the inversion of the colours, but the proportion is constant and together with all the evidence I have gathered already on this model relating to natural phenomena and aesthetics, I am pleased to call this crucial part of the theorem: the Rainbow Proportion.
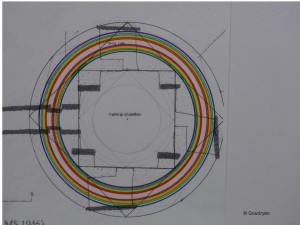
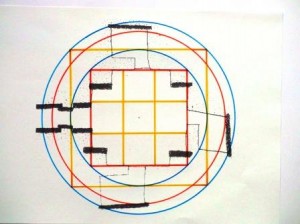
It became clear to me that Stone Age man may have been aware of this Rainbow Proportion within the Celestial Proportion (below, inner blue -red circle) which comprises the full transformation cycle, because he found it reflected in his mathematics of circles within squares within circles…and then squaring his circles… and finding fundamental ratios as 14 : 11. The proportion is not only conspicuously present in the design of Maeshowe, where it can be found in circular alignments of cell-corners,
but also in the Ring of Brodgar, where it is the relation of the stone circle proper and the outer perimeter of the ditch and it is even in the design of Stonehenge where it constitutes the earliest phase of the monument, that is, the ratio of the diameters of the Aubry Holes circle and the platform edge, 11 : 14, (86.43 : 110.0 m, Burl), with the bank, without the ditch, this about 3000 BC, some 5000 years ago. Stonehenge’s early phase is roughly contemporary with Orkney, where though still no really firm data exist.
This proportion even applies to an excavation drawing of two curb circles of cairn H at Carrowkeel (Ireland), again the double rainbow (and the theorem). Possibly a maternity clinic.
The (Rainbow-) proportion forms part of the mathematics which underlies the designs of circles and squares and which hold just this proportion as a matter of fact. Note its perfect proportion as a ring 11: 14 ( as area 1.618… above)
The question of whether the builders were aware of this correlation and subsequent connection between their mathematical model and the rainbow, can never be answered with certainty probably; I myself have been using the model for 11 years without noticing the analogy, until it struck. I am though inclined to think that they also were aware just because they had a far keener eye with regard to nature than I have and especially because, as in Maeshowe (see picture, enlarge!) it is a feature in the design which is not visible at all, but only becomes apparent once one analyses the ratios and symmetries of the design and how they took pains to get all information in, but it is the essence of the mathematical theorem, so it can never be completely clear if they were aware of a connection, but its recurrence points in that direction. No doubt the use of the geometrical harmonies in building was seen as auspicious because it embodies numerical harmony and, as in this case, aesthetic celestial perfection. I have no doubt they regarded their insights in mathematics as deeply spiritual or even divine revelations.
To those who will maintain that people can build mathematically by intuition without knowing that they do, I would say that I am not un-sympathetic to that position when it would regard a single building and only few mathematical ratios would be involved; after all, I have proof that this mathematics is found elsewhere in nature and could be part of our innate knowledge of the divine, which mathematics is to a certain extent, think only of music, but to find it again and again in distant, far apart places is at least remarkable. I found some evidence of the same proportion in an intuitively recently copied ancient-made stone circle and square in Colombia. The point is mainly the ‘stone circle and square’ combination and the possibility to generate the theorem from the ratios.
When 4 major works are obviously in accord with the theorem and, as in the case of Stonehenge, most relevant data can be translated into the model, yes, are key numbers and ratios of the model and consistent with the data from Orkney, where sometimes even the same lengths as at Stonehenge appear, then to maintain that coincidence is the overbearing factor as an ‘explanation’ defies statistical odds. The model’s fit and meaning is irrefutable on the basis of the accepted scientific data, which are all provided by esteemed professionals. The only other option is a Divine Hand guiding them in the execution of the building and me in finding the mathematical key. My data are sound, I don’t cook the books. It’s amazing.
To maintain against the odds that this is all coincidence or ‘intuition’ is far more ‘nonsensical’ than to consider they were aware of this theorem and indeed did use the same units of length, the more so because, in fact, it is a basically simple and straightforward empirical model and the units of length were ready at hand anywhere, for being related to human bones, as I have shown (Bone Measures).
That it seems all rather incredible at first sight, I can very well understand, I still hardly believe it myself, but this is basically because of my own prejudice about what I am inclined to think they could know, which though is culturally defined; in the end I have become rather convinced because you cannot deny mathematical and factual proof, certainly not when it is just because it does not suit your personal views or shakes the very foundations of your own belief system or worldview. This is science, this is mathematics, and mathematical proof, this is not some kind of fancy fantasy.
The only other option is that they unconsciously worked by archetypical geometric truth or as I fancy by shamanic transfer.
For me there has emerged a strong additional argument in that: if I can do it, without being a mathematician (or today maybe just because I am not) and by solely employing logical reasoning on ’empirical’ facts, the ‘natural number ratios’, that then they could do it; this is the more so because I found it all on my own, while they worked probably for hundreds of years with many and bright heads in a tradition of empirical mathematics, which this model in principle is.
So let me begin by showing why it is an empirical model, that is, a model based on experience with measurements, observations and logical reasoning.
To begin with, we know, for one thing, that Stone Age Man was capable of setting out proper circles, which is the majority of stone circles, we also know he was capable of proper spacing although this may be less evident in many circles, but it is evident at the Stones of Stenness and Stonehenge, objects under investigation here. Paradoxically the perfect spacing of Stenness is accompanied by an imperfect circle (which may be two different half circles though), whereas at the Ring of Brodgar nearby, the opposite is the case, there the roundness of the circle is perfect but the spacing seems a mess, which, though, I have argued (Brodgar documents), may be a very deliberate series of well-defined different spacings.
Here it should be noted outright that we cannot expect the kind of precision we associate with traditional mathematics given the means and the material our Stone Age people were dealing with; besides that they probably did not care so much about the precision of their execution as long as the mathematical principles, as expression of Heaven, as intention, were sound. Elsewhere I will point out how understandable it is that in the execution things went wrong.
At every stone circle the questions that came first were: how big are we going to make it and how many stones are we going to place, or the other way round. There are many instances of a certain number of stones with very different circle diameters and also the same diameters with very different numbers of stones. In many places the stones may have been spaced just on sight, without real calculation, but then still they had to have an idea where to place the stones before starting to dig their holes. I think that in general the bigger the stones, the more calculation went in beforehand. Here we are only interested in that category: big stones and/or big circles, major works.
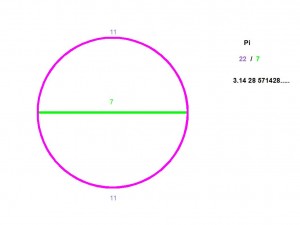
At one moment in the early days of circle-setting the question must have arisen as to how the length of the radius or diameter related to the circumference, because of the question of the spacing of the stones in the circle. This is the question of Pi. I have ever read that mathematicians have given their verdict that the pyramid builders could not have known the approximation 22/7, because this would be too sophisticated a knowledge for ‘those people’. Since then it seems archaeologists don’t take anything seriously that is said in that direction anywhere by anyone, whatever the circumstantial evidence. The problem with mathematicians though may be that since high school they haven’t worked with compass and ruler, let alone that they have ever set out a (big) circle in the field.
 In the reality of the field, though, our circle setters would have found out quite soon that, after dividing their diameters in 3, in 4, in 5, in 6 equal lengths and comparing these lengths to the circumference of their circles, that one day they divided the diameter in 7 equal parts and, lo and behold, this length went exactly 11 times in the half circle, that is 22 times in the full circle circumference. Pi was born as 22 over 7. (=3.14 2857…;pi=3.14 1592…) This approximation is so precise that before there were calculators engineers used it in all their calculations on paper and their bridges still stand; it is within tolerance.
In the reality of the field, though, our circle setters would have found out quite soon that, after dividing their diameters in 3, in 4, in 5, in 6 equal lengths and comparing these lengths to the circumference of their circles, that one day they divided the diameter in 7 equal parts and, lo and behold, this length went exactly 11 times in the half circle, that is 22 times in the full circle circumference. Pi was born as 22 over 7. (=3.14 2857…;pi=3.14 1592…) This approximation is so precise that before there were calculators engineers used it in all their calculations on paper and their bridges still stand; it is within tolerance.
In this same way probably the ancient Egyptians found all their Pythagorean (3,4,5) and near-Pythagorean triangles in the field, just by trial and error, or by chance (20,21,29), not by mathematical reasoning! This is maths still as an empirical science!
I expect that once this complete model is understood and applied professionally it will cause a sea-change in science; but that will only show later on. What I am going to tell here is still harmless and fun. And remember, we are only dealing here with natural (whole) numbers and all our approximations concern differences of thousandths, and often much less, (always capable of resonance).
The following is the absolute crux of the mathematical model. It is this discovery which triggered 11 years of practically non-stop work on this model and brought me in regions I could not have dreamt of ever exploring when I started out, but I remember well the excited moments I found myself saying: ‘This is big’ .
How big it is I still have no way of judging; it still grows by the day, but I know it should not go lost again, please give it the attention it deserves.
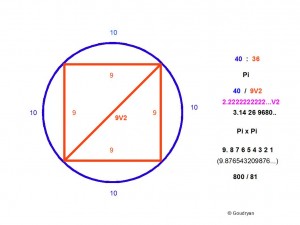
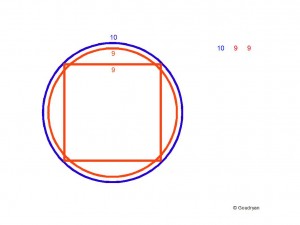
Just so as it is possible to put the ratio of half a circle and its diameter in the approximation 11 : 7, so it is possible to put the ratio of a quarter circle and the side of the inscribed square in the approximation 10 : 9
This results in a different value for Pi than 22/7. The new Pi is 20V2/9 or 2.22222…V2 (3.1426980495….) , which squared is 800/81 or 9.87654321 (9.8765432098765432098..), Pi squared, which brings us back to the natural numbers, that is here, rational numbers (x over y; x/y). This model is not only an aesthetics of geometry it also produces remarkable numbers like 1.2345679012345679012… (no 8 indeed!, but with reason). These repeated sequences of numbers are called periods.
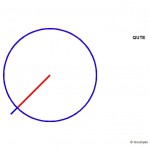 This new value of Pi I have coined: ‘Qute’. It is cute.
This new value of Pi I have coined: ‘Qute’. It is cute.
Its symbol is a mirrored Q; a blue circle with red radius which sticks out + 1/9 (or is it 1/10 ?) in blue, the stake is coming from the centre of the circle, which divides the stake in 9+1=10.
The next step is the big step. We square the circle by circumference, not by surface area, which is an essential difference, and thus we create a circle with circumference 36 (9), this means that the radii of the two circles with circumferences 40 (10) and 36 (9), also stand in the ratio 10 : 9.
This ratio holds for every circle squared by circumference (not area!), in our system: this square’s diagonal is equal to the diameter of its circumscribed circle, which circle relates to the original circle as 10 : 9
These two circles can be seen as part of a sequence of evenly spaced concentric circles, with radii : 1, 2, 3 ….. 9, 10, 11……..18,19, 20.
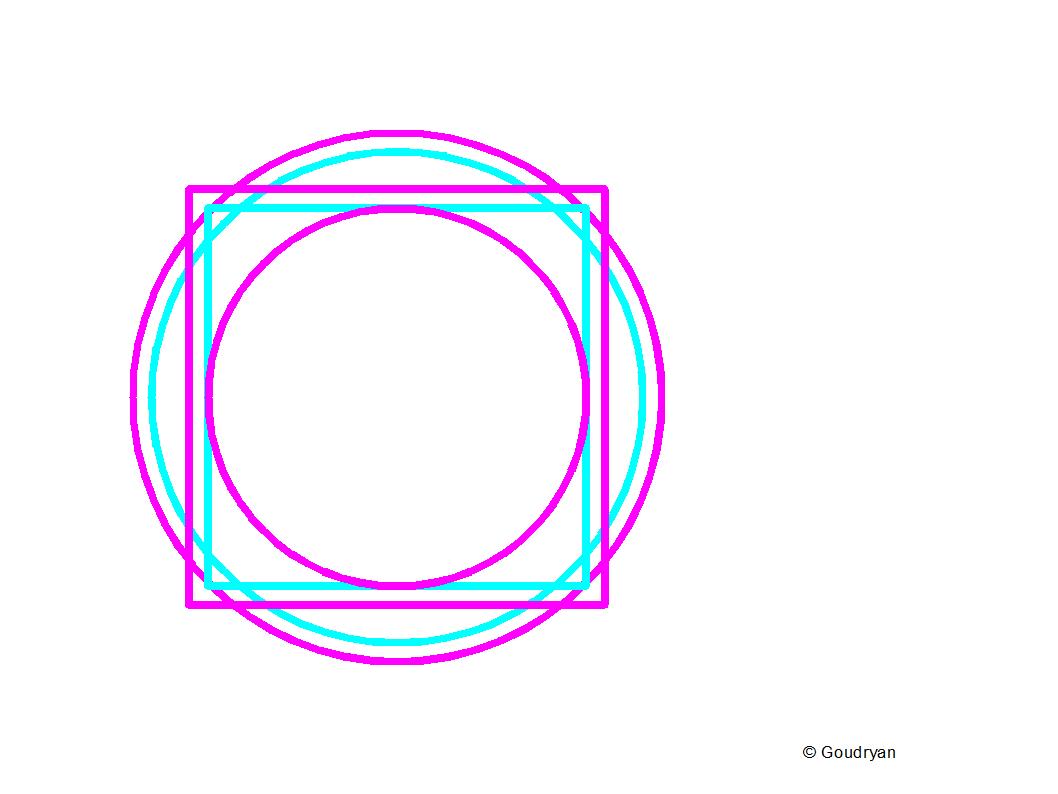
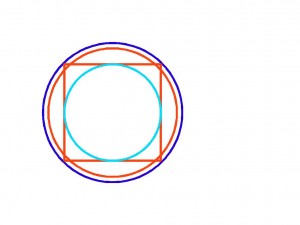 We know that the inscribed circle (turquoise) of a square relates to the circumscribed circle (dark blue) in surface area as 1 : 2. So the dark blue circle is twice as big in area as the light blue circle. ( Here indeed: area)
We know that the inscribed circle (turquoise) of a square relates to the circumscribed circle (dark blue) in surface area as 1 : 2. So the dark blue circle is twice as big in area as the light blue circle. ( Here indeed: area)
Remember, we deal here only with ratios, so we can attach our numbers to diagonals, diameters, radii, perimeters, areas, it makes no difference, as long as we are consequent in our use.
Because the surface of the circle is πr² we take the big blue circle to have a value of 10×10= 100, so the little circle being half, is 50, the red circle is then 81 (9×9) because the ninth square fits perfectly in the tenth cirkel. ( Pi is constant and irrelevant).
The red circle area thus relates to the small circle area as 81 : 50, which we can also write as 162:100 or as 1.62:1.
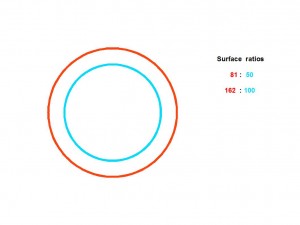 We see here that the ratio 1.620 : 1 approximates the golden section (some say: divine proportion) or Phi, which is 1.618… : 1. (This is the Rainbow proportion by area). Because of the vagueness of the rainbow edges, it is just as well to claim it expresses the divine proportion by surface area. It is a vagueness that mathematicians may abhor, but that may then also be the reason none of them has ever come up with this perfect model of natural number approximations ( or was laughed away).
We see here that the ratio 1.620 : 1 approximates the golden section (some say: divine proportion) or Phi, which is 1.618… : 1. (This is the Rainbow proportion by area). Because of the vagueness of the rainbow edges, it is just as well to claim it expresses the divine proportion by surface area. It is a vagueness that mathematicians may abhor, but that may then also be the reason none of them has ever come up with this perfect model of natural number approximations ( or was laughed away).
When we want to know the ratios of the diameters, the radii or circumferences, we only have to extract the root of our surface values to get to our 1-dimensional values, because Pi is a constant in πr² .
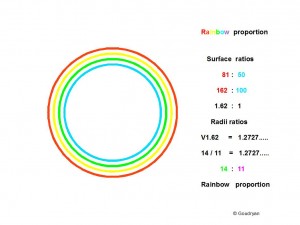 [This picture only symbolizes the double rainbow because it is technically not possible to do it properly in this computer program, the picture of Maeshowe (above) shows the double rainbow with inversed colours]
[This picture only symbolizes the double rainbow because it is technically not possible to do it properly in this computer program, the picture of Maeshowe (above) shows the double rainbow with inversed colours]
Here we see that the square root of 1.62 is 1.2727 92… which is practically the same as the rational number 14/11, which is a period number 1.2727 272….
The difference is less than one/ten-thousandth! It is because of these extremely small differences that the model works, also in reality, which though is not of our concern here.
Important here is that we see that the 2-D area ratio 1.62 : 1 of the ‘Ten over Nine’-geometry can be substituted in the ‘Eleven over Seven’-geometry by the 1-D ratio 14 : 11, which is the Rainbow Proportion.
QED
(Quod Erat Demonstrandum= what was to be proven)