The Creation of Time

La metrologia non e scienza, e un incubo
(metrology is not a science; it’s a nightmare).

G. De Sanctis

Preface

Metrology is the science of the ratios of units of measurement through the ages. Notwithstanding the ‘desperate’ opening quote above, metrology has been the object of research for many great scientists of the past, like Newton and Kepler, people who still marvelled at the knowledge of antiquity. Newton felt he was ‘standing on the shoulders of giants’; where do you find that attitude in science today, how many have ever read an ancient philosopher, who actually themselves were the first scientists? Very few I bet.

In these pages I set out what I think is possibly the oldest system of metrology known to emerge from antiquity, coming from Stone Age Orkney. It may seem highly speculative, but then wait with your verdict until you’ve seen the facts.
An unexpected development has led me to decide adding another unit of measurement to the ones I already had and which all interrelate mathematically.
This new unit is not of necessity per se, I had noticed the unit before, but had no function for it, nor any need. New investigation in recent weeks however suggests it is in a sense the crown on the whole system.

More than the other units, this unit is a concept, I have not yet found a geometrical reason for it, which does not mean there is none, but the unit sort of completes and unites the whole system and is very practical.(See for the units-system chapter: ‘The Neolithic Bone Measures’).
The unit kind of imposed itself on me; as I have stated before, in this system the numbers themselves lead the way. This unit adds to the basic 9 : 10 : 11 ratio of our system a new ratio 8 : 10 (4:5), integrating the numerical cube (2^3=8), but also a new ratio 9 : 25 (=3^2 : 5^2, squares!) emerged, or equally 36 : 100, by connecting to the Megalithic Yard.
It was possibly seen as a pure cosmic unit, this one, because it did not arise from a geometrical necessity as the others, it had arithmetical qualities and it seemed to have strong aesthetical and spiritual overtones next to being practical, it was the unit which became eventually universally known as the ‘foot’, because it so well suited the human proportion, but was always slightly bigger than the real human foot. Being a cosmic measure, it was not really derived from the foot, but from the number 10, the harmony of Heaven.
The Pythagoreans revered the number 10 as the perfect number of the universe. (see Tetractys)

Maeshowe and the Pyramid

The Stone Age metrology I have ‘unearthed’ in Orkney lay buried in the circles of Brodgar and the intricate squares of Maeshowe and the Ness of Brodgar’s Structure-1 and it turns out to be the same ‘natural number geometry’ which is in the design of the Great Pyramid, and the Third Pyramid. To have found the blueprint for Giza in a 9-number system is one thing, to find exactly the same match in Orkney is bewildering. I am like you, I could not believe it…., but eventually I had to and tell you.

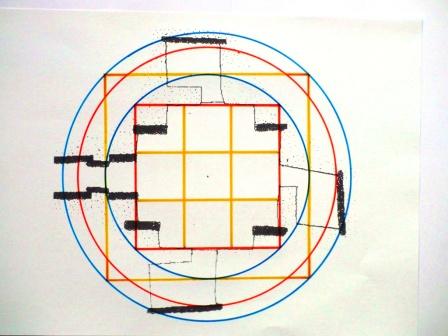
Rainbow Proportion and 9-square in design Maeshowe, the big yellow square is mathematically analogue to the base square of the Great Pyramid, and in perimeter equally related to the red circle, the Earth.

I developed my natural number geometry (see chapter: Pyramid Geometry) on the basis of a nine-number system, which I thought to discern in Sumerian cuneiform tablets, possibly from about the same period in history. I was also totally unaware of matching designs in Egypt, let alone Orkney.

The simple whole number logic and geometry, I developed, based on integrating the ratios 10/9 (1.1111…) and 14/11 (is 1.2727 2727…)(= virtually 0.9V2 = 1.2727 92…) I have explained in many pictograms and texts on this website/book. These ratios are what it is all about, because these whole number ratios produce the basic resonances of nature, of sound, of anything, since ‘all vibrates’. They signify the primal or Ur-vibration, the Ur-sound, Nada Brahma, and it needs only a handful of wellknown primes to pin the logic down.

Flinders Petrie

From my study of the dimensions of the Giza Pyramids I had distilled my own measure for the Egyptian Royal Cubit (RC), to be 52.36cm, and this is where metrology kicks in. During my research I found great use for the rational numbers 189/361 (0.52 35 45…) and 100/191 (0.52 35 60….), they became the perfect tools to crack the measurement data of Giza into whole numbers. (also the Borchardt/Cole value = 0.52 35 5 .. which maybe the best real approximation), but because I wanted a ‘neat’ number I chose 52.36 cm as my standard measure length for the RC in Giza and the Megalithic Ell in Orkney.
It turned out later that 6 x .5236 = 3.1416 = Pi !  And even 5 x .5236= 2.618 = Phi^2.
This is an unusual coincidence, but given that 2 x 99 x 0.5236 = 103,67 m, here coined the ‘Cosmic Length’, it becomes enigmatic
It happens to be virtually the same value Flinders Petrie (an undisputed authority) underlined in Nature (1933):

If we take the natural standard of one day divided by 10^5, the pendulum would be 29.157 inches at latitude 30 degrees. Now this is exactly the basis of Egyptian land measures, most precisely known through the diagonal of that, ‘squared’, being the Egyptian double cubit. The value for this cubit is 20.617 inches, while the best examples in stone are 20.620±0.005inches= 52.375m

(20.617 inches = 52.36 71 cm, which is virtually the same as my 52.36 cm; 29.157 inches = 74.058cm, which is again rather ‘exactly’ my double Remen of 2 x 37.025 = 74.050cm, given the margins of 0.005 inches. Eventually F.Petrie chose for 52.375cm as value for the royal cubit on the basis of the King’s chamber measurements and is followed by many archaeologists unfortunately (because the King’s chamber was built years later and possibly measured with the then pharaoh’s personal hieroglyphic cubit, forearm+stretched hand) As regards the Royal Cubit, this was the measure used in the Khufu sarcofagus and that has a height of  2 x RC = 1.0472m, this not the measure FP proposed, but it must be said that we are talking about differences of just half a mm, which is only over greater lengths a significant difference, not in a sarcofagus. I am sure all these lengths differed anyway on tenths of mm because the differences are so small. Then a choice must be made and I show below that this measure seemlessly connects with all classical measuring systems in whole number ratios.

I did not know Petrie was into pendulums (mind you, in Nature!) but I welcome his unexpected support since we are talking about the same era (ca.2600 BCE) and principles of measurements. I have inferred the pendulum in Maeshowe (2700BCE). Orkney is just earlier and we can be sure they knew the pendulum. (It is one possible use for the famous, but enigmatic, carved stone balls of northern Scotland from those days, easy to wrap a rope around, with the grooves and make it swing.
I also fancy them as being used for hunting game, entangling their wings and legs with 2 or 3 balls on a rope in a slingshot, possibly a matter of skill, anyway, much used in antiquity (David,Goliath), also in war (Romans), so the few beautifully carved balls may have been ceremonial weapon like a later sword, and used in pendulums as well.

It was in Orkney that I found out that my chosen Egyptian cubit length seamlessly fitted Orcadian dimensions in an astounding way, the exact same basic numbers and ratios of my system were here set in stone, again. Moreover the study of the Orcadian ratios made me aware of the fact that the number 0.5236 times 6 = 3.1416, which is Pi ! (3.14159…) and that on top of that 0.5236 times 5 = 2.618, which is Phi-squared (2.6180….; Phi = divine proportion/ golden mean  1 : 1.6180..).
It is that kind of number and this was how I got it, it was just a gift, a lucky choice. And unshakeble now, because the whole metrology of antiquity is commensurable with it in meters.
( 5236  its primes are 2,  7, 11, 17, which is a treasure trove of early primes  2, 7, 11, pivotal numbers in this geometry, its reciprocal is 1,90985 (1.91), this is virtually equal to 21 : 11 (1,909090… =) , the ratio between volumes of sphere in cube in our system (7/11) as (3 x 7/11).
It’s just amazing what this number holds out of the blue!!

The calculator 

Let me here again present the system to show its logic and geometry. Although it started ‘empirically’ with finding the best fit for the data, its precise arithmetical merits have made it into a fixed calculator which governs the seemingly incommensurable ratios of circle, square and diameter/diagonal in natural numbers (1, 2, 3, 4, 5 etc.)

mathematical relation of bone measures

The Ell (2 ulna bones m.) (see picture) is the diagonal of an inscribed square with side 1 Remen ( 1 fibula bone f.)(see Petrie on relation Royal Cubit and Remen, above) in a circle and thus the diameter of this circumscribing circle and the Megalithic Yard (2 tibia bones) is the half circle over the diagonal/diameter of 1 Ell (ME), so 2 Yards (2MY) form the full circle circumference with 1 Ell as diameter, thus 2MY/1ME equals Pi as 22/7, from which follows that 1Yard relates to 1Ell as 11 : 7 , which means that  7 Yard = 11 Ell (beware the inversion); the Remen (fibula bone) is the side of the inscribed square, so the half  M.Yard (1 tibia bone) is the quarter circle over the inscribed square side (remen), and relates thus -> tibia : fibula = 10 : 9, this means that 2 tibia being 1 MYard relate to the fibula being 1 Remen as 20 : 9, which means that 9 Yard = 20 Remen (again the inversion) and this way all their values are geometrically interrelated and their ratios expressed in natural numbers (see Neolithic Bone Measures)
This is the reason that Pi in our system is expressed in several serene natural number ratios:

2MY / 1ME   or

20ME / 9MR   or

16ME / 9MF

Pi in Stonehenge Lintel ring: 180ME / 81MR (= 20/9. √2 (my Qute), root of 9.87654321 or 800/81)

11MEll equal 7 MYard                    = 5.76 m     ********* 11ME = 7MY

9 MYard equal 20 MRemen          = 7.405 m       ***** 20MR = 9MY

140MRemen equal 99 MEll           = 51.835 m     **** 140MR = 99ME   ( = 100 Nippur Cubit)

This means that the units cannot be changed because they are mathematically linked and geometrically meaningful. The point here is not to fix a certain measure as the only right one, the point is that they used these different units to overcome incompatibility on small scales and that they gave their buildings exactly those dimensions in which the units relate in natural numbers and express the logic of ratios in their system.

Although there is no hope that there will ever be consensus on these matters in metrology (the nightmare!) just because the very copying itself brought the differences which created a ‘cloud of values’ around a unit, I think my system is one of the most reliable and intriguing approximations around. Those in the know will immediately see that the values which the system generates are all widely accepted averages, at least, of the old units, and most often turn out to be the best fitting.

The number 0,5236 (.4 x .7 x .11 x .17) (ME and RC) is, as decimal expression of the length of the RC, the key to a system of approximations of the most crucial measurement units of the Ancient world: the Egyptian Royal Cubit and Remen, the Nippur Cubit and the Roman Foot and their mutual ratios.
The extraordinary thing is that the Megalithic Yard with a correction of 6mm on Alexander Thom’s megalithic yard (82.9cm), to become 82.28cm, is the emblem-factor of this Neolithic metrology; it fits Stonehenge, for one thing, far better than does Thom’s yard of 82.9cm or his rod of 2.5MY  and with much greater mathematical meaning. But it also fits in so many other ways so perfectly, that it is beyond my ken.

A striking example of  the consequence of Thom’s or my yard value is in the Ring of Brodgar where Thom claims its diameter is 125 MY at 103.63m, whereas my value gives 126 MY at 103,67m; we see the end result is virtually the same, certainly in this context of material, but the 1  difference makes my value mathematical, whereas Thoms 125 seems a nice number in our world, but has no meaning in a geometrical context at the time. (126=9×14)

Moving between to-day’s cutting-edge theoretical physics and the apex of Stone Age cosmology, as I have done for years in these pages, is quite a gap to be bridged, it is quite disrupting as well, but the scientific spirit is in many ways the same; it would not be the Stone Age if there were no unexpected teachings and other profound surprises.

Orkney
One of my American readers made me aware of a thesis-study by D. Fraser in the Orkney Room of the local Kirkwall library, which states that the entrance width of passage-ways of Orkney chambers is an average of 600mm, regardless of the type, also entrances in the Ness of Brodgar buildings would have that width, the reader claimed. So I went to the Orkney Room and looked up the 600mm, which turned out to be the average of 50-60-70cm measured widths over resp. 7+8+8=23 sample chambers.
The writer of this thesis-study even commented on the uniform average width of the passages compared to the diversity of the chambers: ‘such minimal variation is rare among the variables of cairn, chamber and passage structure’, he writes.
So irrespective of the chamber type or size the passage was uniform. So what is the reason? Practical, no doubt, like the standard measures of a stair case, based on the human proportion, the function, degree of comfort and space-economy.
Before we start the analysis of the architecture in order to understand the use of the building we first explore the origin of the units of measurement we employ to retrieve coherent measurement data.

Orkney and Egypt
To my amazement my original unit 52.36cm, derived from Giza data, not only fitted Brodgar and Maeshowe perfectly, but produced numbers and number ratios which are crucial to the natural number geometry I propose, which turned out to be the same mathematical model as was used in Egypt, so I changed the names of the units into Megalithic Ell (ME) and Megalithic Remen (MR), because this Stone Age use was slightly earlier; possibly at least one century. The model worked; it still does and has never failed me on the most important ancient structures. That is the mystery; it was earlier than Egypt, but the same. This was the proof of the universality of the used mathematics, but also of the measurement units. This is the mystery. Orkney and Egypt, bien étonné de se trouver ensemble.
[I only partly solved the mystery by tracing the Megalithic Ell back to the el-bow, that is, seeing that the male ulna (ell)-bone of 26.18cm could be the basis of the Meg. Ell (2×26.18= 52.36cm) and that the female fibula-bone of about 37.03cm was suited for the Meg. Remen, but still the enigmatic coincidence of the same mathematical system and of equal units as those of Pharaonic Egypt remains]
To pick up on the entrance tunnels we see the double bone lengths of ulna and fibula, 52cm and 74cm, perfectly fitted the passage widths of the most important chambers. (At Holm Papay c. 50cm, Quanterness c. 75cm, Maeshowe c. 105cm = 2 M.Ell, the last width is exceptional, as the whole building is.) So the rule of thumb could have been: ‘passage-width between 2 ulna and 2 fibula bones’ and in fact it varies, passages would narrow at beginning or end and are seldom straight. The height of the passage at the Holm of Papay is c.80cm is 1 Megalithic Yard (82cm), which is high for a passage. So I could have left it at that, all units were again confirmed in the passages of major buildings.
I am the only one who claims these (huge) chambers were not fot the dead but for the living to survive bad weather conditions. A  small tunnel keeps out the cold form the relative warmth of the chambers . These chambers are so big and spacious because of the air they could hold for substany=tial numbers of people during a grim cold spell. The huge chambers on the small islands bear witness of the length of time they were covered by meters of snow.

Egyptian Foot
The 600 mm tunnel width though had stirred me because it was not according to my standard units, but it fitted the specific unit I had left out of my system since I had already three units and saw no function for it in the geometry, moreover it was too spectacular to be taken seriously anyhow. It was apparent in Maeshowe though, and about 30cm, which could do the trick if the Ness of Brodgar data were convincing. It might be time to have another look. The spirit was out of the bottle.
The value of 300mm is the notorious Egyptian Foot of, indeed, 300mm (or is it 299.2mm = 4 palms) and ‘where the Egyptian Foot appears, there the Roman Foot of 296mm is near’, as Newton observed. What is this 29.6cm? It is 1/10 of 2.96 metres, which is 1 perch = 2 paces = 4 steps = 8 Remen, that is what 2.96m is. It is not just another length, it is embedded in a classical system. The step is obviously based on the Egyptian double Remen of 74 cm, the one Petrie took as his starting length!, the pace 2 steps = 1.48m, 4 steps, the perch is 2.96m and this is 8 Remen and indeed 10 Roman feet. From this 8 Remen then 1/10 was taken so that a ratio 8 : 10 was created between Remen and Foot. This is the way the Roman foot must have been created. What links it to the Stone Age? Stonehenge!. As others have noted before, Stonehenge’s diameter is c. 29.62m which is exactly 100 Roman Feet. This together with dimensions of Maeshowe, discussed below, dimensions of Brodgar and possibly wider spread use of its multiples in the Ness, has made me decide to add the Megalithic Foot to my measurement system. It enhances its beauty by completion and can do no harm, although it gets a bit crowded.

The cube and Maeshowe
This 2.96m is the height of the original East buttress in Maeshowe, it is the  highest and most ‘pointed’ standing stone, but the 2.96m is also the average width between the buttresses (3.05, 3.05, 2.87, 2.87). The buttresses are all individually proportioned, they are not exactly parallel but pair-wise aligned with the Barnhouse standing stone 1000 MY (823m) away ? pointing towards Ward hill on the island of Hoy, where the midwinter sun sets (see picture below).

Wintersolstice over Hoy 20/12/2007 seen from above entrance Maeshowe

The 2.96m is, as said, 8 Remen of 37cm, which is why it is so meaningful here, since the diagonal of a square of 8 Remen is by definition 8 Ell, which is the diagonal distance between the buttresses. These at first apparently unrelated measures bring in though the number 8 and its square 64, which, as 9 and its square 81, are sacred to Vedic architecture, and therefore possibly have old ‘Indo-European’ roots in number ratios and geometry, which eventually translates in similar ‘cosmic-design’. Their origin may as well be independent, as the ratios arise from the numbers themselves; many different peoples and cultures have similar sacred number symbolisms.
Proto Indo-European (PIE), though, is an ‘agrarian’, a ‘Neolithic language’, which is what makes it so enigmatic. European and Vedic culture must have split only after the agricultural revolution, so, where they were still in contact, is the much debated great question. Europeans went the way of the bull (Crete, Spain), the Vedic culture the way of the cow (India). That is a good in depth characterization. Today we see the result in a rather different state of mind, but we do share common logic and roots of language.
What happens in Maeshowe by introducing the unit of a foot is introducing next to 8 and 9 and their squares also 10 in the proportion of Heaven, which is doubtlessly appropriate given the logic of the mathematics (the 10 : 9 ratio).

The peak of the capped West buttress

The small picture (above) is a drawing from 1798, whereas the lower picture shows the ‘restored’ buttress ‘today’. We see that the stones are exactly in place up to the old ‘capstone’. The full old picture shows the west buttress is undamaged whereas the south buttress is damaged just at the same top level visible in the fractured wall. The buttresses could support beams, that is, lintels. The wrong restoration of the buttresses is totally misleading.

The crucial point is that the capstone of this West buttress is at height 2.96m as I measured it myself with laser which makes it level with the top of the East buttress’s peaked standing stone (originally then without cap stone) and 2.96m high. The height of the east buttress standing stone is mirrored in the built-up height of the other buttresses, obviously this could, connected with lintels, form a cube of edge 8 MRemen, equals 10 MFeet. The buttresses could also sustain beams to suspend a pendulum and/or a wooden floor to store grain etc.

Maeshowe: Multi-purpose House of Heaven

The numbers 9 and 81 appear in the 9 Ell (4.71m) side of the 81 square-Ell ‘ground-plan’ of Maeshowe (including buttresses). In my story of a scientific culture around Maeshowe and the Ness of Brodgar a very heavy pendulum would be kept swinging in the space of the imaginary cube, within certain circular boundaries and give a measure of time and circular movement, like the pendulum in the Pantheon in Paris. [The longer the rope of the pendulum bob, the longer its all- over swinging time and the heavier the bob the lesser the disturbance by a gentle push (to keep it going)]

Maeshowe is the Temple of Time in my (pre-)history of Western Europe, the Ness of Brodgar its Academy and Center of Standard Units (Metrology). I know this is highly speculative, but not impossible and it expands on Alexander Thom’s vision, which I did not take seriously myself at first, but also Euan Mackie follows Thom’s ideas, I found out recently as the only authority in British academic archaeology today, it emerges.
I have serious problems with hierarchical and religious overtones (priests) which Mackie brings in, because that is in my view out of character with what we know of shamanic society and customs, but in general Mackie came to very much the same view that I developed on the basis of my findings (he already in 1977); in my view though the Maeshowe culture was one of a scientifically enlightened shamanic horizon, a cultural revolution which possibly even brought an end to the actual power of the shaman, evolving into the shared power of cosmologists, the origin of collective scientific pursuit, a brotherhood maybe, exploring time; both are still seen within an egalitarian setting, not the elite of Mackie’s (Maya-type) priesthood.
The prophet, the druid, the bard, the artist, the priest, the monk, they all have their origin in the creative and mystic power of the human mind, embodied in the accomplished Stone Age shaman.

It was an open society, without much hierarchy, but for age, and equality of woman and man, as still in Siberia today, ready to admit any dedicated stranger who wanted to join in the cosmological quest. It could indeed have been a kind of monastic setting like Pythagoreans and Tibetan Buddhists ( who are the most scientific-minded Buddhists). The Ness of Brodgar is though not a religious but a scientific centre, a cosmological academy, occupied with the ‘Creation of Time’, as I have set out elsewhere; all its discipline would be centred on making the right calculations for the calendar and setting the start of the seasons and ultimately predicting the eclipses.
No doubt there were seasonal festivities at the Ness.
It should be remembered that the shamanic society is utterly egalitarian, the good shaman is a compassionate equal in everyday relations, nothing sets him or her apart, but for their wisdom and healing power. A ‘primus inter pares’ is the best description maybe. Shamanism is not a religion, it’s a practice, the shaman is not a priest who conducts a ritual, s/he is the ritual, s/he is primarily a healer of body and mind. Truly enlightened people seem often very ‘ordinary’, like you see it in the Tibetans, who are in spirit and power probably closest to the shamanic embiance and the ‘enlightened’ Stone Age cultures.

I think I owe it to my extraordinary findings in Orkney and to our Atlantic ancestry to strive to ‘prove the improbable’; it was and is a great exercise in penetrating ‘time’ and the ‘timeless’, in entering the past to find eternal truth (mathematics), and I am grateful I was bold enough to give it a try and take all the consequences. I persist to this day.

Cubes found at the Ness
It is noteworthy in this respect that at the Ness of Brodgar, my proposed Academy site, a stone throw from Maeshowe, this year two differently sized stone cubes were found, typically man-made, they measure, about 5 and 8 cm cubed. The small one is a regular sharp edged clear cut cube, with circularly hollowed sides, the bigger one is smoothed but definitely a cube shape again and also a hollow side.
Now please don’t underestimate what it means they knew the ‘cube’ as concept. This is the proof that my projected cube inside Maeshowe is no fancy, they damned well knew the shape, it’s a measured thing. This was around 3400BCE, half a millennium before Giza was built in Egypt.
I guess they were standard weights, their relative size and weight could be interesting. But no archaeologist is interested in this approach. Mathematics? Don’t make me laugh!

Cubes from Ness Brodgar

 

The concept and even ‘reality’ of the cube is now firmly evident in the archaeological record of the period in Orkney(3500BCE-2200BCE) (the Isbister-cube, earlier found, is less cube than these cubes) and it supports my envisaged ‘abstract’ cube in Maeshowe, the concept was definitely known, as said.
As far as I can find out no cubes are known of the Neolithic Age elsewhere. Square and cube are ‘abstract’ mathematical concepts, directly related to circle and sphere; and most of all to symmetry.
In Vedic (temple) architecture the square is a sacred symbol of perfection. As far as I know no other buildings in megalithic architecture are based on perfect squares as are Maeshowe (2 squares, 3 circles, concentric) and now, close by, Structure-1 at the Ness of Brodgar, my Lecture Hall (at least 4 double squares, 4 crossing circles, Vesica Pisces, possibly hall with pendulum). Also this unique groundplan is not recognized by archaeologist, although I put it before their eyes. Is this science or ‘threatening’.

Rationalizing √3
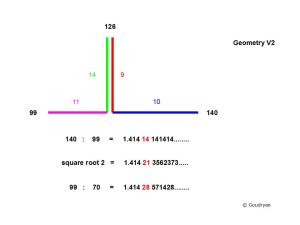
Because the diagonal of the cube is a square root 3 (√3) of the edge, we analyse it within our system so the following is a good example of how to rationalize irrational numbers and make them suitable for the system. This usually is achieved by changing the second and third decimals (with thousandths only) and by fixing a period of usually 2 digits, which, multiplied by 99 or 198 produce an approximate whole number [99x 1.414 2135…(√2)= 140.0071….but 99×1.41414141…=140]. Thus the data become part of the system.
We ‘streamline the data’ by ‘manipulating’ the thousandths and less to create whole numbers and their ratios. This is allowed because of the margins of resonance and tolerance in reality. These are the ground rules, the key to the system to transform irrational numbers into systemic harmonics of ratios, rhythms and resonances. This, I believe, is how nature works and calculates…., this might become the solution to quantum uncertainty. (a mighty insight if right) 

We return to the cube in Maeshowe and now the question is whether the 3-D diagonal of our cube, which in ‘normal’ mathematics is the irrational number √3, being 1.732050…, can be expressed in a whole number ratio, like it was done with √2 by rationalizing it to the twin 140/99 and 99/70 and their average 19601/13860 (= 1.414 21356 4..213564..)
Usually the best result is given by accommodating 99, which is done by creating the best fitting double digit period, so in the case of 1.7320…. we choose 1.732 32 32 32…., which provides us the ratio 343 : 198.
This equals  7³ / 9×22 and is nothing less than a ‘dream ratio’, and that with √3! (again only our ‘pivotal’ numbers involved)
From this we can now construct a cube with only natural numbers, with an edge of 198, a square diagonal of 280 and a cube diagonal of 343, all in the same unit of length.

(picture)

Don’t underestimate that the cube-diagonal is multiple 7 which makes it immediately rational as diameter of a sphere enclosing the cube, by Pi as 22/7. This sphere has circumference: 343 x 22/7 = 1078, (r=171.5) with a volume (4/3.π.r³) of 21,137,603.67 (= factor 11) whereas the circumscribing cube of this sphere is 343³, which happens to be 7 to the power 9 = 40,353,607. (7³³).
We can now also find the ratio of the volumes of inner cube : outer cube = 66 : 343 , in natural numbers,  because ratio volume inscribed cube to circumscribed cube is 1 : 3√3 and 3√3 = 5.196 1524…… and 343/66 = 5.196 96 96 96… which fulfils the ‘rule of a thousandth difference’ easily. There is absolutely no flaw in this logic, it’s exhilarating again and again for what it achieves in transparency.
So we have extended our natural number geometry all the way from ‘square in circle in square’ to ‘cube in sphere in cube’, it covers all three spatial dimensions and all this always with the same factors 7, 9, 10, 11. (2, 3, 5, 7, 11)
This system never lets you down. It is rock solid and beautiful. (Beauty is Truth)

√3 : √2  ‘rationalized’
In our unit system we can follow another strategy to rationalize the √3 by defining the ratio √2 : √3. That ratio is 1 : 1.224744….,which is then transformed into 1 : 1.225, being 80 : 98, or 40 : 49 (mark here 7² again), as easy as that. (This is again within the rule of the ‘free’ third-digit options. This rule here also enables 1.222222… = 11 : 9, important, which, no doubt, can be useful on occasion, this is fully within the rules and it supports the system, but closest and best here is 1 : 1.225, I think now, although √ 2 : √3 = 9 : 11 or 81 : 99 is too beautiful to discard, and so is 80 : 98 . I hope the reader will get an understanding of my ‘enthousiasm’ for this system, which is completely built on the first 6 primes only! (2, 3, 5, 7, 11, 13)

Since we know that √2 is in our model of Maeshowe the diagonal of 8 Ell, we then know that this length multiplied by 10 serves us 80, needed to relate to the 98 in the ratio 80:98 for the √3 . Like in the case of √2 -> (9.9/7 = 99/70) we need a factor 10 to reach integer relations here for 9.8/8 to become 98/80 or 49/40. This way we have another irrational relation transformed by factor 10 into a ratio proper to include in our system, that is √3 : √2 = 98 : 80 = 49 : 40, for any unit ( also 99 : 81 = 11 : 9).

The Megalithic Foot

The introduction of another unit of measurement may seem to weaken my case because this way one of the units would always fit any length, one could object. This objection might be justified in case my units only just always fitted the Neolithic lengths in whole numbers, but that is not the decisive point of my argument and the strength of my system, the proving point of my system is that: all the designs express fundamental mathematical ratios and geometries according to this system and that it is statistically ‘impossible’ to achieve that fact by chance.

My analysis of the Neolithic data shows that the heart of natural number mathematics is expressed in real lengths, constructed out of key numbers in the rational relation of circles and squares, as expounded by me. The enigma is that these ratios precisely express the system I had developed theoretically through a nine-number system, which happened to also fit Giza; another mystery. I am probably myself most perplexed by what it all reveals.

I do not need the Megalithic Foot to prove my point, but I can no longer neglect the 100 Roman Feet of Stonehenge’s inner diameter now that it emerges that the Megalithic Foot also completes the Ring of Brodgar theorem in a magnificent way, because its  103.67m diameter is exactly 350 Megalithic Feet which results in a stone circle circumference of exactly 350 x 22/7 = 1100 Megalithic Feet. It is an emblem of Pi as 22/7 and reminds us of the grand design of Giza and its crucial number 11 in the Great Pyramid proportions (side 440 RC, volume 11x Third Pyramid).

A Cosmic Length

It is this pivotal Neolithic work, the Ring of Brodgar, of which the diameter 198 ME (103.67m) exactly fits the ground-square of the Third Pyramid, which holds the same key ratios of cosmic harmonics. This is even more striking when we realize that the dimensions of the Great Pyramid express the ratios of the Globe, its radius expressed in the height and its circumference in the square perimeter. Its circumference of 921.45m is (approx.) half a minute of arc, which actually implies that, because of the crucial Pi- relation between Third and Great Pyramid, it must be derived that also Brodgar expresses the circumference of the Earth one way or the other in whole numbers. And it does it indeed in a peculiar way since 8² x 6 x 10³ (=64 x 6 x 1000 = 384000) x 103.67m gives the same earth circumference as the Great Pyramid at just over 39,800km. (921.45x2x60x360) (so less than 200km off the mark, not much more than the French mistake by 70km nearly 5000 years later 150 years ago, coincidence?).

This product of 64 and 6 and 1000 reminds us of the analysis of Maeshowe and its square of 8 Remen between the buttress edges = 64 and its 6-sided cube of 8 Remen and of a (10x10x10=) 1000 MFeet³ in the same cube. So Maeshowe would hold the numbers and ratios by which to calculate the circumference of the earth with the real cosmic-length of Brodgar’s diameter. So there would be cross-referencing between these two close megalithic sites, as in Giza between the Third and Great Pyramid. (Third at eastern platform level)
This length of 103.67m, equal to 280 Megalithic Remen, and to 198 Megalithic Ell and to 126 Megalithic Yard and to 350 Megalithic Foot, this one length is an enigma in its own right, because it combines 4 (even 5) different ancient units in one length, expressing Pi in many revealing ratios.
The length occurs at Maeshowe? (henge diameter I once read!), Brodgar, Newgrange, Avebury, Great Pyramid and Third Pyramid (side) and it is multiplied by √2 = 146.61m, which is the original height of the Great Pyramid, more importantly, it shows up in the distance from the King’s Chamber floor level to the top of the Pyramid, 198RC, and it is the side of this pyramid at air shaft exit level, where it marks the Third Pyramid’s dimensions as the top of the Great Pyramid. I can’t help it. It is even exactly 200 Nippur Cubit, to make it worse for the sceptic ( the fifth unit!).
These are all accepted or derived  values (Legon), except for my inference for the side of the Third Pyramid, Menkaure, which nobody has ever mentioned as possibility even, but that value is obviously a ‘free for all’ by now with rather differing assessments by the professionals, so it is totally up to the reader, to decide on, because it will always be contentious, I’m afraid. For me the consistentie of the geometry is paramount, the ‘plan’.

Cosmic Length
This is why I call it the ‘Cosmic Length’, maybe it even occurs in South America or elsewhere. The question then is: was it born from scientific knowledge, or related by ‘divine inspiration’ in a shamanic setting, or do we have to believe all this was done ‘unconsciously’ as some archaeologists would have you believe, as if that does not pose an even bigger question? They create an even greater enigma to feel they can’t help they don’t know. Anything then but admitting their subject of study knew more than they do themselves.
It probably was a mixture of science and ‘divine inspiration’, as often happens in science.
There is no higher precision, no greater cosmological vision, as early as that of the Atlantic Megalithicum, I think. Creating the logic of these diameters and circles, packed with mathematical and cosmological meaning, may be the lasting scientific significance and historic greatness of Stone Age Orkney as the most prominent and influential Neolithic legacy of the British Isles. This unique quality positions this partly drowned archipelago as the most likely origin of both the legends of Hyperborea and of Atlantis in antiquity, there just is no better, historical, candidate, but I think few will follow me here soon.

The ratios

So far the Megalithic Foot was not yet related to the Megalithic Ell, but that is taken care of in the Ring of Brodgar itself where the radii are now as follows in the 4 different units:

MYard —–MEll—– MRemen—– MFoot

–63———- 99———– 140———— 175

This then summarizes in the following ratios relating to the Megalithic Foot

8 MRemen equals—- 10 MFoot = 2.962——- 8MR = 10MF

9 MYard equals—— 25 MFoot = 7.405——- 9MY = 25MF

99 MEll equals—— 175 MFoot = 51.835—–99ME = 175MF    (=100 Nippur Cubit)

All these numbers present the same value as the radius of the Brodgar Ring at 51.835m
and we recognize the numbers of the diameter and ring when we multiply:

126 MY = 126 x 0.8228 = 103.67m ***** 126 x 22/7= 396MY

198 ME = 198 x 0.5236 = 103.67m

280 MR= 280 x 0.3703 = 103.67m ***** 280 x 22/7= 880MR

350 MF = 350 x 0.2962 = 103.67m ***** 350 x 22/7= 1100MF

The Megalithic Foot now enables us to create the significant symbolic circumference of exactly 1100 units, related to the 350 of the diameter, 11 and 7 united with tens and hundreds. This completes the whole theorem in its cardinal ratios.

Giza
Again we can appreciate the mathematical kinship with Giza in the circumference of Brodgar as 1100 MFoot = 880 MRemen which is in meters 325.82m. The diagonal of the Great Pyramid is 880 Remen, by definition, because its sides are 440 Royal Cubits.
880 Remen is also the circumference of Brodgar, the mentioned 1100 Foot, ergo the circumference of Brodgar is equal to the ground diagonal of the Great Pyramid. The same unit of length is applicable, since we have seen that Petrie’s quote on the Remen makes clear that the Royal Cubit is virtually identical with the Megalithic Ell.

The mathematical relations between Giza and Brodgar are then the following:

The circumference of Brodgar is 880 Remen which is the diagonal of the Great Pyramid. (325.82m)

The diameter of Brodgar is 280 Remen , 280 being the number of RC in the height of the Pyramid at 280 Royal Cubit. (146.61m)

The diameter of Brodgar is 198 Megalithic Ell (=198RC), this is equal to the distance of the Kings Chamber floor level to the peak of the Pyramid, 198RC exact. (See superb work on Giza by John Legon). It is also the side of the Third Pyramid and the side of the great Pyramid at airshaft level.

The diameter of Brodgar can also be expressed as 126 MYard, while the height of the Third Pyramid is 126 RC = 65.97m, (Lehner: 65-66m) which is also the height of the top of the Pyramid rising from the level at 154RC of the King’s chambers air-shaft outlets, 126 RC, true! (154+126=280) (Legon). The Third Pyramid being exactly the top of the Great Pyramid and virtually 1/11 of its volume. (as far as I know no one has claimed this before)

The height of the Second Pyramid is 274 RC (=143.47m), which with the 126 RC of the Third Pyramid added makes 400 RC (by all means better than the only alternative 399). (another new claim)

The diameter of Brodgar is 198 Megalithic Ell, this is equal to the side of the Third Pyramid (Mycerinus, Menkaure) at 198 RC = 103.67m, thus the circle of Brodgar ‘exactly’ fits within the ground square of the Third Pyramid.

The diagonal of the Third Pyramid is 280 RC (also with Lehner’s data!), this is equal to the height of the Great Pyramid.
Giza is one great ‘cross-reference’ design.

Menkaure, the key Pyramid

By all means Menkaure’s diagonal will always remain so close to the height of the Great Pyramid (even allowing Lehner’s approximate 196 x 200 RC), that it would be stubbornly silly not to assume it was intended to be the same length, the more so because diagonals were very important to the Egyptians and Giza is a ‘Grand Design’. This all relates mathematically as has been convincingly shown here and by several others as well. Menkaure holds in fact the crucial ratios of the ‘geometry of square root 2‘ as I have named it long ago.

Diagonals can hold the Pythagorean ratio and are the diameters of the circumscribing circles; all very understandable.
The circumference of the Third Pyramid is 4 x 198 = 792 RC, that of the Great Pyramid is 1760 RC, which is a ratio 9 : 20, important in Pi as 20/9 x 99/70 = 22/7 and 20/9 x 140/99 = 2800/891, two of our rational substitute values for Pi.
This 20: 9 – ratio relation between Great and Third Pyramid has never been observed yet, as far as I know, it makes the Third Pyramid the mathematical prototype, that is the key theorem of the Great Pyramid: so again ‘primeur’ here.
Elsewhere I showed already that the volume of Menkaure relates to Khufu as virtually 1 : 11 [(280×440^2) : (126×198^2)= 10.974 : 1] and since Menkaure is the top 1 segment of the Great Pyramid it means the rest is 10, so as ratios  1:10 and 1:11.

Continuously the same numbers keep revolving in this design, its richness in ratios seems endless.

Conclusion

So what we see here is an uncanny match between two World Heritage monuments of approximately the same period in history, (2700-2600 BCE), designed by two completely different cultures but expressing exactly the same mathematics with exactly the same type of ratios and even exactly the same units of measurement.

How is this possible? But also, who is going to challenge these results?

You will have to change the following data, because the math is solid as it is.

Unit of length 52.36 cm confirmed by F. Petrie’s Royal Cubit of 20.617 inches = 52.367… in ‘Nature’ (1933) = 1 Megalithic Ell (ME).

Diameter Ring of Brodgar: 103 metres and 60-70 cms (Burl, Thom, Renfrew), 198 ME= 103.67m

Height Great Pyramid: 103.67 x √2 = 146.61 metres = 280 RC (481ft), equals the diagonal of the Third Pyramid (even with the improbable 196x200RC in Lehner’s data)

Circumference Ring Brodgar: 325.82m, (with Pi= 325.69) virtually equals the diagonal of the Great Pyramid (Cole data: 921.45/4 x √2= 325.78m).

Floor level King’s Chamber to peak Great Pyramid : 198 RC = 103.67m , is diameter Brodgar. (The Cosmic Length)

King’s Chamber air-shaft exit level at 154RC is exactly 126RC below the peak of the Pyramid (154+126=280). 126RC is the height of the Third Pyramid which is, thus, by design (incorporated in) the top of the Great Pyramid and the mathematical key to its proportions.
The complete mathematics surrounding Pi as 22/7 is in Menkaure ((4 x 198) / (2 x 126)) in the smallest natural numbers!.

To sum up the mathematical grand design of Giza as a whole we can conclude that Menkaure expresses the ‘rationality’ of square root 2 and of Pi, Khafre represents the Pythagorean triangle and Khufu symbolizes the Earth as Globe and the Heavenly Proportion of Harmony, based on ratios 7 : 11 and 9 : 10 .

Who has the authority to change these fundamental data? Nobody ever will, because it is the best data we’ll ever get, unless the original design of Giza is found on papyrus ( since earlier key survey benchmarks, that Petrie used, are gone now).
When you are not convinced by these clear facts, then still you owe the magnificent Megalithic buildings and their builders a kind of ‘benefit of the doubt’, since you cannot refute these facts, however incredible they may seem.
I think the brainpower of the Neolithic cosmologists, and their Egyptian pseudo contemporaries for that matter, was beyond what we see today because it also sourced from the world of ‘superhuman’ faculties like shamanism, where the whole of reality is ‘animated’ in a mystic union with nature and ‘cosmic information’ becomes available for the extraordinarily trained, inquisitive and receptive mind of the shaman.

****

This piece is continued at Metrology 3:  ‘Giza and Orkney’, and Metrology 2: ‘The Crucial Question’ on the passage-chambers.
There is a related piece with confirmation of the inferred radii of the design circles of Maeshowe by laser-measurements and the recurring length of the diagonal between the buttresses in the chapter ‘The Measure of Maeshowe’