The Creation of Time

******** Mathematics at the Ness of Brodgar

Preface 27/10/12

This is an improved and enlarged version of the same page I published 2 years ago on the Ness of Brodgar, a conglomerate of many big buildings from around 3400 BCE in Orkney. I am still working on other things archaeological but this page on Stone Age mathematics and geometry still is as important as it was when first published and better documented now. It is rather technical but also understandable when you like doing a toddler’s puzzle. A much easier and wider ranging explanation can be found in the blog I wrote at the same time, called ‘Ness of Brodgar Blog 2010’. (you can read that chronologically, but also going back in time). There you can follow how it all developed and what I came up with at the time.
The piece below shows how the design of Structure-1 of the Ness of Brodgar is thoroughly mathematical, double squares, and turns out to be even calendrical! Besides that it is a formidable confirmation of the value of the Megalithic Ell.
It is a pity this extraordinary find, like the squares, circles and triangles of Maeshowe which you can find elsewhere on this site (The Measure of Maeshowe), are not appreciated by archaeologists the way they deserve. The mathematical facts I found about both sites may be as important, if not more, than what they found so far. They find ‘things’, artefacts, I discover numbers and mathematics.

Introduction

This piece may be rather numerical and technical for the average reader, though you can appreciate the fit of the pictures which are all true to scale, just skip some text, if it gets too much, but read the end parts on general ideas and parallels with Vedic culture (see Vedas)

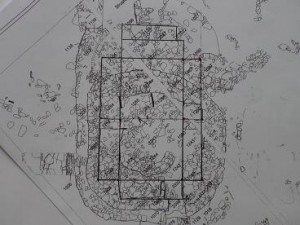
Structure-1
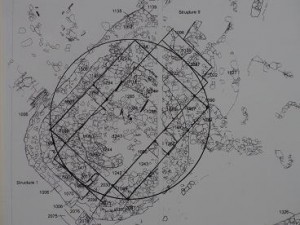
Above are the double squares that I have found in the design of Structure-1 at the Ness of Brodgar. The measurements I give below are in human ulna, fibula and tibia bones, resp. 26.18cm, 37.025cm, 41.14cm (see Bone measures), although I have come to believe that they probably also used half units of these bone lengths, at least the half ulna length, because I think they did not have a concept of a half number, but did have a concept of a half and a double unit of length. In the human body bones of 13.1 cm  would fit Powell’s contention, that they used 13.1 meter! as a unit in building Newgrange. I found that the clavicle would fit 13.1 cm, that is half the ulna length of 26.18cm, so 13.1m would be 100 clavicles.
Here we see all squares expressed in ulna bone lengths of 26.18 cm. The red squares are 15 ulna = 3.93m squared, the yellow squares are 12.5 ulna = 25 clavicle, 3.27m squared, and the small purple squares 2.5 ulna = 5 clavicles (0.655m). Significant here is that the piers, which are the double small squares, that mark the recesses, are practically rectangular while often these piers taper towards the inside as we see it at Structures 8 and 12. So the rectangular character has largely been preserved in the piers, which have a length of 5 ulnas = 10 clavicles = 1.31m. (on the aerial photos it seems the piers taper slightly, but this may not be the case at the base).

Superimposition

The next images show how the squares fit (superimposed) in the present foundation, which is aligned exactly north – south, just like Structure-10 nearby.

 

Stone age geometry

The next picture shows how the overall length of the inside is twice the diagonal of the red square, in blue, 11.11m, being 30 fibula of 37.025 cm, and how a Pythagorean triangle (a²+b²=c²) of 15, 20, 25 ulna (3,4,5) can be constructed from the top corners of the piers towards the diagonally opposite corners. The width of the chamber of 25 ulna = 6.55m, reveals itself here and is coloured in green.

The overall rectangle that is defined by the squares, (so without the south and north recesses) is 25 ulna (6.55m) wide and 30 ulna (7.85m) long and thus has a ratio of 25 : 30 = 5 : 6.
Unfortunately the original layout is much damaged by the intrusive later curved wall to the north and the sub-circular intrusive wall in the southern part. One may hope that at least the southern intrusive wall will be removed after being examined, in order that the crucial squares can be restored to their original design and the straight geometry of the building can be appreciated. In a sense this part of the building is even sharper in finish than Maes Howe and has a different mathematics and geometry to show.
This building needs to be studied intensely, both by archaeologists and mathematicians together, this building probably represents the pinnacle of Neolithic thinking and intellectual capability.

Squares and circles again

In the pictures below we see how circles can be drawn in Structure-1, which have all the same radius of 15 ulna bones= 3.93m, and we see this same measure return in the distance between the piers in Structure-8 (in the lower right hand corner of picture), but also in the south recess of Structure-10 (following picture), which is reminiscent of the south recess of Structure-1, so a doorway may be expected there.

These similar measurements definitely point to contemporaneous building. Contemporaneous in my view is a time span of maybe 25 to 50 years at the most, say, a generation (or two?).

I can show now that also a circle was involved in Structure-1, its centre being in the middle between the north corners of the opposite piers. Its radius going through the major rectangle of 6 : 5. The point is that this circle touches on the south wall of the south recess, which now turns out to have a depth of 1,18m or 9 clavicles of 13,1 cm in the SW corner. Note that the deep north recess probably had ‘two depths’ as shown on the plan, but the wall is rather damaged there.

Still smaller units?

The following analysis shows why I think the half ulna bone length, the clavicle, was another standard length.
When we calculate the radius we do this by squaring the square side length of 15 ulna, now 30 clavicles and by the squaring of the half width of the chamber 12.5 ulna, now 25 clavicles, so 30 squared + 25 squared = 1525, and the square root of this is 39.05 ulna, which is the radius of the circle through the corners of the rectangle and which is practically a whole number, the overall difference being 5 cm !!! (39 x .1309 = 5.105m, 39.05 x .131= 5.11m), which is trivial. This is empirical, not theoretical, this is what they measured! This is still experiential geometry.

The Clavicle
I found to my surprise that the average clavicle is 13.1cm, half an ulna bone, the sought-for measure, so a general bone has been found! This clavicle measure seems to be widely used instead of the ulna in this design, let alone the megalithic yard, (each to the measure of its design, like we do (m , cm, km), which would be a strong hint that they treasured whole numbers in their ratios (like we do) and this is a relatively small building. (why would they not use the most convenient measure within their definite system, they liked half lengths, because they could not calculate with half numbers.
39 is 3 x 13 and 13 is an important factor in calculating the calendar, as it is 28 x 13 + 1 = 365, which gives the number of days in the year and 9 x 13 +1 = 118, which is 2 x 59 = 4 x 29.5 , the days in the lunar month, so 118 is the number of days in 4 lunar cycles of 29.5 days. (the number 28 returns in the measures)
Keep this in mind, the number 13 was popular in the Hebridean stone circles, as well.

Below a picture of the circle and its tangent south wall.

 

Pythagoras at the Ness of Brodgar

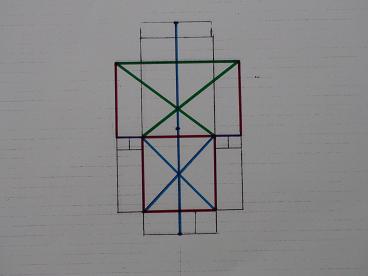
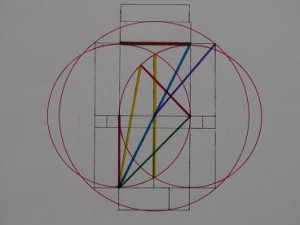
Below we see the most striking thing of the design of Structure-1, the Pythagorean triangles which constitute square roots 2, 3 and 5 in approximate whole numbers. The same that holds for the radius, just explained and calculated above, also holds for the diagonal through the double square, here in blue, this is always square root 5. (the double square we find also in the basic design of the King’s chamber of the Great Pyramid)
The double squares in the centre have a side of 15 ulna, 3.93m and are unit in this design, here in red with number 1. The green line is the diagonal, so square root 2, this is 15 fibula, 5.55m, the yellow line is square root 3, which fits exactly between the intersections of the two circles, this is also mathematical fact, Vesica Piscis, but we can see the length appear as hypotenuse of the three coloured triangles with sides: unit 1, in red, square root 2 in green and then of course the yellow line is square root 3 ( 1 squared + square root 2 squared = 1+2=3, thus the square root of 3). The yellow lines do not intersect, but do have the same length.

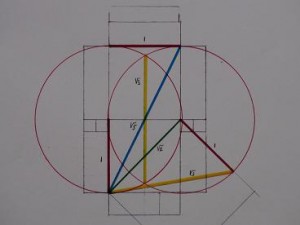
Structure-1 Ness of Brodgar Vesica Piscis

The point I am making here is that again the chosen numbers produce near-Pythagorean whole number complexes. I do not claim they knew these mathematics, but that they by trial and error got whole number ratios. Precision is an obsolete concept dealing with megaliths. The concept counts.
As follows:

For unit we use not 15 ulna, but 30 half-ulnas, the clavicles, so double the unit is 60 clavicles, the length of the double square, the width is one unit, is 30 clavicles, so the the square root 5 length, the blue line, is the square root of the sum of 60 squared + 30 squared = 4500, which, lo and behold!, is 67.08, another near whole number, the prime 67, with only a difference of 8 mm in the overall length, again trivial in dry stone walling, and well within tolerance of any house building, being about the thickness of the plaster of your walls at home. It took some time but I found the use of 67 in our calendrical application and not just ‘some use’ but related to the 173 days period of the eclipse. 67 + 67 + 39 = 173. This is Thom’s ‘danger period’ of the eclipse and it is also related to the returning prime 43 (Stones of Stenness, Stonehenge) since 4 x 43 +1 = 173.

The same method can be used for the yellow line as square root 3. Unit, red, is 30 again, the green line as square root 2 is then 30 square root 2, both squared and added give 900 + 1800 = 2700, of which the root is 51.96, which is practically 52 = 4 x 13. (52 is the number of weeks in a year in our calendar, so the whole diagram is still valid today, which is rather extraordinary, I think).
According to this analysis crucial data in the way of Heaven were incorporated in the design of this extraordinary structure, which is most worthy of being restored to its original design and be preserved as such. But to preserve the integrity of this extraordinary gift of the Stone Age, let’s please wait for a generation of archaeologists that knows how to collaborate with mathematicians, without feeling overwhelmed by the idea that these are ‘the real scientists’, as they think of themselves. (Structures 8 and 12 do not have that finesse or mathematical meaning as far as I can make out now).

Multiples of 5 and 10

So what we find in the chosen dimensions of this building are all full or near-Pythagorean triangles all based on dimensions in multiples of 5, the fingers of a hand. This is the first ‘decimal’ building I find in Orkney, but 5 and 10 arise clearly from the measurements of Newgrange.

Below is an other arrangement, which shows how all these mathematical relations could be set out in the plan of what I call, the ‘Lecture Hall’. It could even be that the points where the circles intersect were marked on the floor, which would be 60 – 52 = 8 divided by 2 is 4 clavicles = 2 ulna = 1 Megalithic Ell = 52.36 cm from the horizontal base of the main rectangle. It all fits. The purple line is the radius of 39 clavicles.
The clavicle = 13.09 or from now on 13.1 cm, would be unit to this building, and is 1/100 of the 13.1 metres proposed by Andrew B. Powell (Science or Symbolizm?1994) as standard for Newgrange.

I do not mean to imply with all this that they were aware of arithmetical squares and square roots, what I do want to stress though time and again is: that whole numbers, or near whole numbers arise constantly from the calculations of their geometry translated in ratios, that mathematically or calendrically meaningful numbers constantly come forward and that what they did, is : measuring in whole numbers, with specific units of length, designed to even out incompatibilities and incorporate them in their designs. That their ‘straight’ lines still are slightly curved may be because exactly straight was deemed weaker and less stable which is both true.
Everybody marvels at the craftsmanship of this original building.

Chance?

It is in my view statistically impossible that I keep finding these meaningful ratios in all the buildings by chance; I am not a magician, all the data are there for anyone to check. This is Stone Age mathematics, just because it is meaningful.
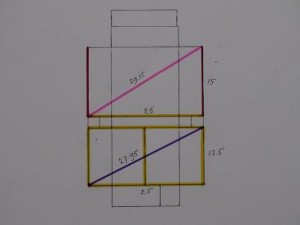
The following picture shows again meaningful numbers. The diagonals in pink and purple are both close to whole numbers 29 and 28.
29 belongs to the arithmetic of the moon cycle as 29 + 29 + 1(or 29+ 30) = 59 = 2 x 29.5 (days of the moon cycle) and 28 as 4 x 7 (female fertility cycle), but more importantly as half of 56 which we find in the Aubrey Holes at Stonehenge, which are widely seen as signifying 3 big moon cycles of 18.6 years = 55.8, nearly 56 years.

Here it becomes clear why I always emphasize the whole number approach, because instead of 12.5 ulna, 25 clavicles would, with 50 clavicles, immediately produce 55.9 as diagonal and point to 56, so all the crucial numbers involved in the moon and sun calendar are represented in this geometry by its ratios and are still valid today. This is all not theoretical but experiential geometry.

 

Mathematical sketches

The photo below, which is a piece of stone found in Structure 12, shows a definite triangle at the left, with possible ‘double squares’ inside. The squares are here unmistakable. It is a worn sketch, but it shows how they were aware that a rectangle produces similar triangles when drawn in a bigger triangle. It is not Pythagorean, but rather close, it is a quick sketch. This is not decoration, but representation and possibly calculation. (the longest line is about 4 cm). The ‘arrow-point’ drawing counts 10  fairly visible parallel lines, and maybe a grid of 100 rhombuses  was intended, but the superfluous triangle with another 2 parallel lines which then rests attached is unclear, but certainly we see a grid that could aid counting; it may even be a precursor of Grooved ware decoration!

Boyne Valley again

Often I overlook things because there are so many numbers to memorize but it is rather noteworthy I think that the overall width of the chamber of Newgrange between back-stones C3 and C14 of the side recesses, is 6.55m (O’Kelly 1982). 6.55m is the width I have calculated for Structure-1, it is 50 clavicles or 25 ulna or 12.5 Megalithic Ell.
What is more is that Powell also suggests a unit of length of c. 11.10 m for the design of Knowth, this is exactly the 30 fibula (37.025) 30 x 0.37025 = 11.11m, of the overall inside length I have calculated for the ‘Lecture hall’. Also the calculating in fives and tens is the same as Newgrange according to Powell’s research.
The link with the Boyne Valley gets again confirmed by these similar measurements.

I am confident that my model stands, even when it turns out that the unit of length on site is slightly different from the model. I won’t change the model, because it is perfect as it is, it is a tool, a calculator, rather than an infallible empirical fact, and it has not got to be more than a very close approximation of the actual units used on site, which may have differed slightly from site to site anyway, people have different sizes ( then we are talking 1-2 mms per bone, not more, but they may add up).

The Neolithic Ice Age (NIA) (4000-2900 BCE)

What makes my theories scientific in a sense that is still not common in archaeology is that they can be verified and falsified, which is rare in megalithic archaeology, where unprovable theories are the order of the day. The problem with that is that it provides little knowledge in a scientific sense, for instance the argument moving away now again from the established scientific character of, for instance, Stonehenge, back to funerary emphasis, the same happens here at the Ness of Brodgar, without a human bone on the scene. The firm association of megaliths with funerary practice is a ‘deadly’ one in archaeology. It stifles any theoretical progress. The funerary use of chambers occurred when their primary use as refuges was over, which, on any scale, was only after 2900 BCE, when the thousand year cold spell, the Neolithic Ice Age in Europe, was over. (end of megalithic Funnelbeaker culture)
When two skeletons are found in a cist under the wall of a house in Skara Brae nobody thinks of a tomb, but every human bone found in a megalithic chamber ‘confirms’ it was built as a tomb. And it wasn’t. Skara Brae shows unequivocally that burial was a domestic affair.

The confusing thing over and over again is the enormous time span of these communal centers, always ‘open to the public’ (as a refuge should), their different phases and the subsequent lumping together of evidence from completely different periods and even cultures. These sharp Neolithic minds would be saddened by the total incomprehension of modern archaeologists regarding their skills, their knowledge and their daily lives. (extreme weather conditions)
They were a lot smarter with their mathematics than your average archaeologist I’m afraid. The question is: are these up to their job?

Ratios are artifacts

What I want to stress, over and again, is that carefully considered numbers and dimensions which hold definite ratios, are also facts, hard facts, and artifacts in their own right, they don’t change even in 5000 years in many, and at least in the most important, cases.
The only one till this day, who was bothered about the mathematics of the stone circles was Alexander Thom, not an archaeologist, and now me, not an archaeologist either, whereas these are the most outstanding, sophisticated and abstract expressions of their culture. Still the exact number of stones in the major circles at Avebury and Brodgar is not known in 2025. It is not a priority for archaeologists, although excavating a stone circle for locations of stones only is not such a big (intrusive) thing since it can remain rather on the surface with today’s technologies.
The idea that the number of stones could be of importance, even crucial, does not occur, it seems, although to make a calendar you need to calculate and keep records, that’s clear. It’s all too far-fetched for ‘sophisticated’ archaeology

How did they calculate

This obvious problem of how Stone Age man calculated is the central theme of archaeology on this website and I think I have found the solution, but no one seems interested. It is too much like translating the hieroglyphs without the Rosetta Stone: impossible, though the loads of mathematical facts I present speak for themselves. I was lucky to have the guts to try the Egyptian Royal Cubit (52.36 cm) consequently on Orkney’s megalithic buildings and data.
I show conclusively this model of mathematics can be applied successfully, that is, meaningfully and is not beyond ‘Pythagoras’ in difficulty, although it is further reaching in content because it deals with circles as well.
A 14-year old can understand this math. But indeed it is not your ordinary math, but neither is ‘Megalithic culture’ your everyday exotic culture: it is the birth of science in the West, most probably.

The stones of Brodgar or the walls of Maes Howe don’t move, nor go away (at least let’s hope so), neither does the overwhelming circumstantial evidence, nor a verdict beyond reasonable doubt; new terms to archaeology perhaps, but well worth considering, in a situation where mathematical precision does not and cannot exist beyond what I present.
And what is more, is, I think, that we owe this extraordinary culture a strange ‘benefit of the doubt‘, that they indeed could do it.

The matching measures!

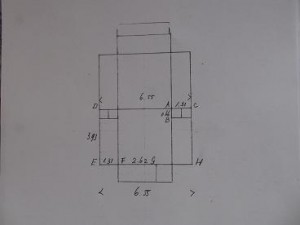
Below a plan with capital letters to show which measures I have taken on site by laser.
The picture shows the predicted measures, the list then shows the readings from the laser. The readings are either spot on, or differ by no more than 2 cm, less than an inch.

Below laser readings with in brackets the predicted value:

laser
AB = 0.66 (0.66)
AC = 1.31 (1.31) this is the east pier, which is rather intact yet

DC = 6.57 (6.55) this is the overall width of the chamber measured again at
EH = 6.57 (6.55)

DE = 3.91 (3.93) this is the side of the big square, that is doubled

EF = 1.31 (1.31) this the depth of the recess and equal to AC depth

FG = 2.62 this was a surprise, but is the same as 3 recess measures in structure-8, which were all 2.64 as measured last year , 10 ulna bones is exactly 2.62; note that EF +FG = 1.31 + 2.62 = 3.93, the side of the big square.

How can anyone ever hope to do better than this in a 5000 year old building (or even in a new one today!) This is again full proof for the validity of my units of length and most probably for the design of double squares.

The importance of Structure-1

Structure-1 of the Ness of Brodgar provides a great opportunity to find a unit of length used at the site because it is so precisely built, but has some peculiarities now that I have seen it from close-by. Unlike Alexander Thom, I do not think that the unit of length was as absolute exactly the same everywhere as he claims, but I do agree with him wholeheartedly that they aimed at using whole numbers and that there was a center where the unit of length was kept as a standard. This was Orkney and the idea is that people from all over the British Isles and even maybe further afield, came to Orkney to gauge their units of length with the standards of Orkney and compare their pulses, their natural wrist watch, against the standards of the number of seconds of the Brodgar Ring.

That is at least something I am prepared to consider seriously because of the uniformity of measurements all over the British Isles and beyond.
When I first read this idea of Thom’s about such a center, I thought it far-fetched but my own calculations and measurements give me now every reason to think he may have been right, because Orkney is so exceptionally sophisticated and everything fits meaningfully.

I have added the measure of time, the pulse, which is quite a leap of the imagination, but then, the passing of the stars through their opened roofs (proof at Wideford) is related to a concept of time and distance, of speed, a vivid awareness of the movement of the cosmos, and possibly the earth. Others no doubt may well find this concept of time too far-fetched in turn, but maybe they will eventually change their mind, as I did regarding Thom’s claim. These were true cosmologists, these were the first true all-inclusive thinkers, but closer to the shaman than to religious or scientific hierarchy. This is about the harmony of Heaven, a mystic outlook, which one cannot possibly associate with cold astronomical science or rigid dogmatic religion as we know it today

After the Rainbow Proportion which immediately relates to the celestial sphere, yes, is part of the Celestial Proportion (see elsewhere), we find here again a geometry which relates to the heavens and holds, in an exquisite geometric construction, all the crucial numbers to calculate the sun cycle, the moon cycle and the eclipses.
The cosmological impact of all this is clear enough.

Vedas
In Vedic literature it is said:

‘The Universe is present in the Temple by means of the proportion’

‘If the measurement of the Temple is in every way perfect, there will be perfection in the Universe as well’

(The Veda’s are the sacred texts of the Hindus and are in Sanskrit, an Indo-European language; Veda= knowledge , in Old German = wetan, in Dutch= weten, in German = wissen, English = wit, wisdom)

Another striking similarity is the use of the squares of 9 and 8, with the number 81 and 64 associated, regarding the Vedic temples; exactly what I found for Maeshowe.

Reader, I am not a New Age apostle (if only I could believe in a New Age, I would be less pessimistic), and I am myself probably more amazed about what I find than anyone else. This geometrical calendar is beyond anything I had ever expected of finding just weeks ago, but as so often it is Stone Age man himself who in his choice of proportion leads me to his incredible knowledge and discoveries and speaks to us through these proportions. Math is a language, but without words. It speaks through simple harmony and beauty, over ages. It is Prehistory becoming History by a universal language.
The message is received and understood!
The Maeshowe culture celebrated the light of the sun and the birth of a child, not the darkness of the night and the gloom of death.

That is the meaning I get from this culture and like to pass on.