Ramanujan, genius
19/11/2010
Srinivasa Ramanujan was a genius. He was the type of prodigy who seem to have a direct hot line with the Beyond. Mozart is a first name that springs to mind as comparison, but a composer; mathematics and music are though, with mysticism, the areas where one finds prodigies; Krishnamurti is another name.
Ramanujan was Indian and a very religious Hindu. He is quoted as saying: “An equation for me has no meaning unless it represents a thought of God”.
Ramanujan was ‘discovered’ by the English mathematician Hardy who came to rank him equal to the greatest mathematical geniuses ever. He was invited to Cambridge and, after a year of agonizing about leaving his home country, he moved in 1914 to England to live there eventually for only 5 years in which his already weak health deteriorated, probably due to general ‘home-sickness’, which weakened his immunity. He became seriously ill and eventually went back to India, where, soon after, he died in 1920, only 32 years old.
In his tragically short life he nevertheless managed to find a great number of mathematical equations (close to 4000), which prove fruitful to this day.
What interests us most in Ramanujan here is his unconventional and intuitive type of mathematics which was initially only appreciated by a few mathematicians, but seems now to have penetrated into the famous Super-string theory, today.
[[The following is not so difficult to follow as may seem, it is more philosophical than technical and as always: skip the math but keep on reading, because in the end it is not about math but about philosophy]]
Ramanujan showed this rare immediate insight in complex numbers as it is related in the following anecdote about the number 1729, since called the Hardy–Ramanujan number.
The story goes that Hardy once arrived at Ramanujan’s residence in a cab numbered 1729. Hardy commented that the number 1729 seemed to be rather uninteresting, but Ramanujan saw right away that it was actually a very interesting number, being the smallest natural number which can be represented in two different ways as a sum of two cubes:
That he sees a thing like that immediately I can imagine because he is the type of man who does not only know all of the squares of numbers, say under a hundred, by heart, but also their third powers. I know all primes under a hundred instantly and a number of squares, but that is because I have worked with them for years and years now. I recognize the number 729 as a power of 3, but not even of 9 directly (shame on me), and 1000 is obviously 10x10x10, but I would not have seen the 1728 as 12 x 12 x 12 nor do I see the 1 so easily as 1 x 1 x 1.
The point is that I am a bit used to decomposing numbers by adding or subtracting 1 in my model, but I never thought of seeing the 1 as a square of 1 ( like you can in pseudo-Pythagorean triangles, as I realize now) or third power of 1, nevertheless it seems a very similar method. So in that sense I can relate to his immediate insight in this rather simple case, which is more a matter of experience than genius, but still it shows me how completely absorbed by numbers he must have been and the brilliance to see: it was the smallest number with this double quality.
What struck me in Ramanujan’s dealings with Pi, is that he used explicitly numbers central to my geometry, especially 99 and 9801 (99^2), but also 9 and 22 and 19 (9+10), figure, as you will see.
I am just a messenger, not a mathematician, I report on what I find, working my way through the mathematics with a logic I understand, which concerns natural numbers. It is a mathematics I found all by myself and I gave it its own new foundation in logic, in symbols and diagrams. You could also say these mathematics found me (and gave me a new foundation). Only the, to me revealed, mathematics I can grasp to a certain extend, it is in essence the logic of the geometries of sphere and torus, as I understand it, but I am sure it holds much more I will never fathom.
What I found is a geometric logic of the numbers and that logic was my guide, and then there was this revealed beauty around every corner, if I just kept guided by the principles laid down in the numbers.
All these geometries express the harmony of the natural numbers and their resonances and I have come to see the revealing beauty of numbers and geometries myself, so in that respect I see how Ramanujan is one of those rare voices from the Beyond, a ‘Wunderkind’. (wonder-child)
Numbers express a higher logic and this Logic comes to light in Nature as the Logos, the Tao, the Way. (Heraclitus’ Logos). This quality of the Numbers instilled in Ramanujan the conviction that he was dealing with divine truth.
This same awe for mathematics may have given it a sacred ring in some cosmological societies in antiquity even going back to the Stone Age. It was, after all, the key to the Cosmos and its Law.
The geometry of square root 2
The paradox is that we humans make the numbers and yet nature reflects itself in the numbers, so number is our knowledge of nature or maybe how nature expresses its intelligence in us. Mathematics is very much about Truth (yes, capital T) and that is what gives its revelations a ”mystic ring”.
Ramanujan is the perfect embodiment of one who is humbled by his own knowledge and his insights.
Ramanujan had an intricate approximation of π which is
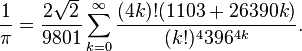
I have no idea what it means but it looks bold and precise.
Written in understandable characters it comes down to this approximation of π:
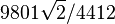
which is 3.141592 73… ( π = 3.141592 65……) so up to 6 digits correct
What you probably don’t, but I do immediately see, is the number 9801 being the square of 99, or 9^2 x 11^2 (9 squared times 11 squared) and I realized, a bit late, that the 396 is 4 x 99. This then combined with a square root 2 involvement comes close to my approximations of square root 2, namely 140/99 and 99/70 and my substitute for π in 2.22222…V2 = 3.14 2696… named ‘Qute’ . ( V2=square root 2)
My other two substitutes for π are 22/7 and 2800/891 (base 9 and 11) which give a product of 800/81 ( 9.87654321), the crucial π^2 of our torus geometry of which 2.222…V2 is the root.
This may seem to have no relation on the face of it but when we continue it comes closer.
{9801 V2 = 13860.70712… note this 13860 because it is 9 x 10 x 11 x 14 , which is 9801 x 140/99 and these are the core numbers of my geometries}
The core logic of the analysis of square root 2 sees the same numbers
******140/99 = 1.4 14 14 14 14 14 14 14…..
(sqrt(2)=V2 = 1.4 14 21 35 62 37 30 95…..
19601/13860 = 1.4 14 21 35 64 21 35 64…..
*******99/70 = 1.4 14 28 57 14 28 57 14…..
What we see is that square root 2 is ‘exactly’ in between the two rational substitutes, together they have as absolute middle the number (140/99 + 99/70)/2 = 19601/13860 = 1.4 14 21 35 64 21 35 64…. (213564 factors : 2, 3, 13, 37), the standard closest rational approximation of square root 2 in our system.
9801 x 140/99 = 13860 = 9800 x 99/70
(9801 + 9800) / 2 x 99 x 140
19601 / 13860
1.4 14 21 35 64 21 35 64 21 35 64 21…..
When we put together 9801 (9x9x11x11) and 9800 (7x7x10x10x2) (only 2, 7, 9, 10, 11) we get 19601, when we divide this by 13860 ( 9 x 10 x 11 x 14) we get the rational approximation of square root 2 up to 8 digits , being 1.414213564 213564 21…. (V2 = 1.414213562…, less than 2 billionth difference.)
So in our system, since it does not allow irrational numbers, the substitutes for square root 2 are 140/99 and its twin 99/70 and depending on the occasion 19601/13860 or even my Ramanujan-type formula which is slightly better than the above, which I give further below.
Here first another of Ramanujan’s approximations of π which more perfectly fits our system
Spoken it runs:
‘The square root, of the square root, of the sum, of the square of 9, plus, the division of the square of 19 by the number 22, in symbols it is
V V {9^2 + (19^2/22)} = 3.14159265 258……. (pi: 3.14159265 358….)
He found this by first squaring the square of π which gives 97.40909103…, then by subtracting 9^2=81 he got 16.40909103…, multiplying this by 22 he got 361.0000027…. ; 361 being the square of 19. This is to a certain extent a process of trial and error, it just happened to fit nicely, but that is not the whole story because it might indicate a deep-structure because of the 9, the 19 (9+10) and the 22, all crucial numbers in the Rainbow Proportion. It is the same way I find deep-structure in numbers, by systematic trial and error until it fits and it always fits in my system, because of its rules. Ramanujan found many of these systems and rules, I think.
In our system we would change the π^4 = 97.40909103…. into 97.4090909090909…… and multiply by 11 and then by 2 to get the prime-number 2143. So my approximation would be a bare π^4 = 2143/22 = 97.409090909…. and π being 3.14159265 258…. , which is exactly the same actual number as Ramanujan’s and in fact based on the same principle of approximation, but what a different presentation in revealing deeper structure, because in his notation the double square root is traceable in the two different type squares, whereas in my numbers their is no hint of deep-structure.
If I though use my method of factorising ‘flanking numbers’ then a new dimension seems to open because it is possible to show a deep-structure relation between the two here mentioned approximation formulas for Pi by Ramanujan (this is a surprise for me, just happened) because they show a deep-structure link in their hidden factors. The prime is 2143, its flankers are 2142 and 2144, note 2×21 = 42 and 2×22 = 44 . Factorized we get 2142: 2 x 3^2 x 7 x 17 and 2144 = 2^5 x 67, then 66: 2, 3, 11 and 68: 2, 17 so here we see returning early primes all very much contained in recognizable numbers, but that is not all, because 2144 is the reverse of 4412 from the other formula of Ramanujan, the prime 1103 from the original formula also turns up (4412/4=1103), so via my approximation system I show a deep-structure relation between two of Ramanujan’s approximations of Pi, which is remarkable and promising.
The crux here is to see that the ..0909103… , where an early sequence …0909… appears, will render a (near) whole number by multiplying with 11 or a multiple of 11 , this is one of the basic approximation rules of our system, which Ramanujan, an expert on natural numbers, no doubt, knew.
The possible problem for mathematicians with my way of operating is that it seems arbitrary, but within the whole system it is not arbitrary at all, it all stems from the rule that differences less than a hundredth, so ‘per milles’, are not fixed (margin of resonance) and that we stick to our key factors, 9, 10 , 7 and 11. ( first 5 primes: 3×3; 2×5; 7; 11)
We constantly ‘translate’ irrational numbers, like ‘Pi’ and ‘V2’ into our rational system, so that they fall within the rules and a smooth rational calculating is secured. This is what makes this way of calculating extremely fast because the solutions are already part of the system, so it becomes more of a search than a calculation. The same holds for factorizing repunits.
There is nothing faster than mathematical necessity, this may be the answer to immediate reaction over great distances in particle physics, entanglement: math is instantaneous.
The universe of mathematics knows no time.
And Nature, as a matter of course, calculates with natural numbers.
My Ramanujan-type formula for the square root of two is:
140 / 99 + 140 / (99^2 x200) + 140 / (99^4 x 2) or
140 / 99 + 0.7 / 99^2 + 70 / 99^4 or
2 x 7 x 10^1 /99 + 7 x 10^-1 /99^2 + 7 x 10^1 / 99^4 =
1.4 14 21 35 64 13 92 05 …….
This is also a rational number with a rather longer period and only slightly closer than the earlier, much simpler approximation above, but this one seems to have definitely more to say on deep-structure.
As with the repunits, this decomposing of numbers may bring deeper structures to light which may have bearing on some yet undiscovered mathematics. So writing complex and irrational numbers in different ways and approximations may be revealing.
Some years ago I referred to my mathematics as the ‘geometry of square root 2’, to give it a name, but this model is in fact indeed proof and explanation of the irrationality of the square root of 2, because of the incompatible ratios of 10:9 and 14:11, which frame the geometry in circle and square as 2-D substitutes for sphere and torus, ratios which are also recognizable in the periods of the rational numbers.
It is significant to see that the period 142857 of 7 reflects its multiples in 14 28 56(+1=57), the same happens at the start of square root 2: 1.4 14 21 35 63(-1=62), where the initial period breaks off and becomes irrational and unrelated. These discernible multiples are unique to the period of 7, so it shows that in the deep-structure of the irrationality of square root 2 the reciprocal of 7 is paramount, which points directly to our system and 7:11:14 ratios.
Another confirmation is recently found in a unique period prime (very rare) which shows definite affinity with the reciprocal of 7 and starts: 142857 and ends similarly.
Geometry of square root two is a more precise description than Rainbow Proportion, as I have called it now, (this is ‘more poetics than mathematics’), but the true theoretical Rainbow Proportion (the geometry of sqrt 2) got its most magnificent man-made expressions in the Ring of Brodgar, in the ground-plan of Maeshowe and in the superb three dimensional ratios of the Great Pyramid; in Nature we see the proportion in the Rings of Saturn; and in the Rainbow itself of course.
Ramanujan’s place on this site has not only to do with the similarity in his intuitive and creative way of analysis or his emphasis on the explanatory power in approximations of perennial mathematical constants in revealing deeper structures between numbers, and mostly natural numbers it seems, but Ramanujan also reminds us of the fact that people can have knowledge that they cannot have acquired in their lifetime through a process of learning and thinking, that this is the spontaneous knowledge that is in all of us, but only in a few breaks free.
It is the nature of the prodigy that they have this knowledge and skill of which nobody understands where they got it from. A Mozart composing at the age of 4 and the like, it always seems incredible and baffling.
In a sense such occurrences always make me wonder about reincarnation, as if some brilliance is carried on from an earlier life, or is it the (partial) incarnation of a godhead of learning like Celtic Lugh, the many-skilled, Greek Apollo or Hindu Vishnu, or just the chance that someone really has the gift to use the human brain as it should be used: to its full potential.
What is important here is to see that people can have knowledge which comes out of the blue and still carries an undeniable truth, it is a ‘cosmic’ revelation. But in general these occur in the one who is also seeking, or involved in exploring the truth.
This is the reason why I think Stone Age man could acquire knowledge especially in mathematics, which is unbelieveable today given their perceived state of development. Shamans in their ‘Rausch’ can do incredible things so when in search of mathematical harmonies of circle and square they could find them because the harmonies are there for the one who searches and eventually recognizes them.
*************